Sometimes in my professional life, I’ll be given the X-, Y-, and Z-coordinates of a set of points that are approximately coplanar, and one of the things I’ll need to do is to find the orientation of the plane (the strike and dip). To do this, I use the following procedure:
Compute the variance-covariance matrix C of the X-, Y-, and Z-coordinates.
Compute the eigenvalues and eigenvectors of C.
The eigenvectors corresponding to the two largest eigenvalues will be in the plane, and the other will be normal to it.
Turning the normal vector into angles is then a matter of trigonometry.
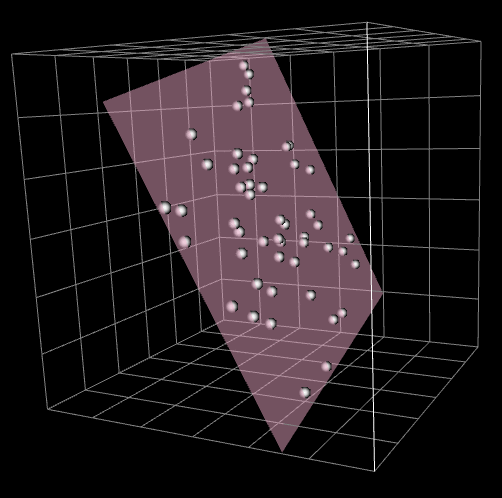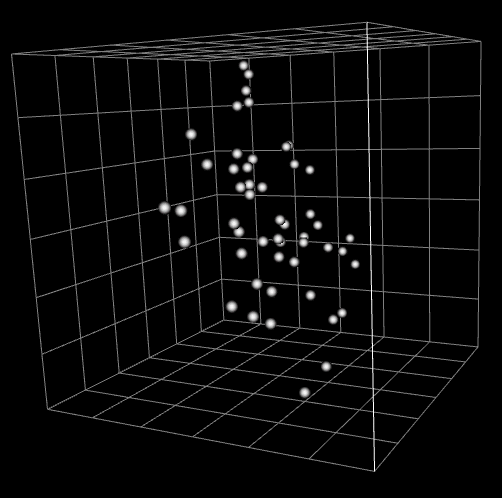
In this post, I want to sketch why this procedure works, how it gave me an intuition for these sorts of eigenvectors, and how that intuition turned out to be wrong when I applied it in a case that was too far from different from what I’d trained it on.
Eigenvectors of the variance-covariance matrix
My understanding of this topic starts with the Wikipedia article for principal component analysis, in particular this graph:
It’s a scatterplot showing a classic bivariate Gaussian ellipse shape, with a big arrow pointing in the direction of the major axis of the ellipse, and a little arrow pointing normal to it. How might we derive those arrows?
We can consider it as an optimisation problem. Imagine rotating the X and Y axes anticlockwise by an angle θ, giving the points new coordinates X’ and Y’ defined by
The goal is to find the value of θ that maximises the variance of X’ (by eye it looks like about 30 degrees). We don’t even need the equation for Y’ here, since we’re just maximising in one dimension, so this seems like a very tractable problem.
But trig functions are annoying, and a single rotation will not generalise easily to higher dimensions. So let’s instead consider a linear transformation of the coordinates
subject to the constraint that
This easily generalises to higher dimensions, and we can even stop thinking about the original variables as coordinates if we want. Suppose we have variables X_i for i = 1, …, N. Then the constrained optimisation problem is to find values u_1, …, u_n that maximise
subject to the constraint
The variance expands to
and introducing a Lagrange multiplier λ for the constraint equation gives an objective function ϕ to maximise of
To find the constrained extrema, we take the partial derivative of ϕ with respect to each of its arguments, and set them equal to zero. The partial derivative with respect to the Lagrange multiplier, by design, simply gives us our constraint back:
The interesting action happens with the partial derivative with respect to u_i. We get
which can be written as
This equation must hold for each i, and is the definition of the eigenvalues and eigenvectors of C, written in component form. The more compact vector form is Cu = λu. One of the eigenvectors of the variance-covariance matrix will therefore give us the linear transform of the variables that maximises the variance. But which eigenvector?
Continuing to work in vector notation, given an eigenvector u of C with eigenvalue λ, the variance of the corresponding linear combination is
So, the eigenvalue is the variance of the linear transform derived from the eigenvector. Maximising the variance therefore reduces to finding the eigenvector corresponding to the largest eigenvalue.
Linear algebra gives us some more nice properties: the variance-covariance matrix is real and symmetric, so eigenvectors corresponding to distinct eigenvalues are orthogonal. The different corresponding linear transforms will therefore have a covariance of zero. This is why you can sometimes do dimension reduction with PCA, deriving decorrelated factors that capture most of the variance of the full dataset.
One note of caution: in PCA, it’s common to standardise the input variables to zero mean and unit variance. This makes sense when dealing with a highly multivariate dataset, where the units and magnitudes of different variables could be very different. But in the motivating problem for this discussion – finding a “plane of best fit” through some approximately coplanar points – it is important not to standardise the coordinates. We want the directions where there’s lots of variance, and we should not standardise this information away.
Using eigenvectors to average directions
Sometimes I have two directions and I need to compute their average. (This will later be a weighted average, but for now let’s consider the unweighted case.) To make the discussion simpler, let’s suppose that these are directions in the horizontal plane, like bearing 030° and 060°, which should average to 045°.
A first problem is that bearings are discontinuous as you cross between 000° and 360°. This is not a difficult problem to solve: convert the bearings to unit vectors, average the vectors, and compute the arctan2(y, x). There’s a Wikipedia article on the circular mean. It has some somewhat counter-intuitive properties at times, but I can let that slide.
Where it gets trickier is that my directions are in fact bidirectional. North is the same as south – the entities I’m trying to average might be better thought of as lines going through the origin, rather than oriented directions. If I have bearings 010° and 185°, then I want an average that is either 007.5° or 187.5°; I absolutely do not want the naive average of 097.5°, which is the worst answer possible, perpendicular to where it should be going.
My first idea was to arbitrarily pick a half-plane, and flip the sign of a vector if it pointed in the opposite half-plane, prior to doing the averaging. If I forced all bearings to be in the interval [000°, 180°), then I would get the right answer for my average of 010° and 185°, since the 185° would be converted to 005° before being averaged with 010° with no problems. But this doesn’t always work: 010° and 170° are both in my reference half-plane, and they would average to 090° instead of either 000° or 180°.
Instead I took inspiration from PCA and all those approximate planes that I’d found in three dimensions. I converted each of my bearings into two unit vectors, one the negative of the other. Here’s a diagram of my 010° and 170° case, with points drawn at 010°, 190°, 170°, 350°, two pairs-of-points:
It now looks like I can usefully apply the knowledge from the previous section about the eigenvectors of the variance-covariance matrix!
Wrong intuition: Let b_1 and b_2 be bearings that are not mutually perpendicular, with corresponding unit vectors v_1 and v_2. Let C be the variance-covariance matrix of the X- and Y-coordinates of the points {v_1, v_2, -v_1, -v_2}. Then the dominant eigenvector of C points in a sort of bidirectional average of b_1 and b_2.
I don’t want to pretend that this eigenvector should be an exact average: it’s minimising squares, whereas averaging is a linear operation. But, you know, it should be pretty close. It won’t work if the two bearings are perpendicular: to get from north-south to east-west, you can rotate either clockwise or anti-clockwise, and by symmetry there’s no reason to prefer one over the other. So something weird should happen when the difference is 90 degrees, but that case is a set of measure zero.
This intuition is not always wrong, but it turns out that the anomaly influences a set of measure much greater than zero.
Let’s fix the first bearing at 000°, and increase the second bearing from 000° to 090°. Let’s also introduce weights, giving the 000° bearing a weight of 1, and the varying bearing a weight of 0.5. Naively, when the second bearing is 030°, we’d expect a weighted average of 010°. Less naively, we might be aware that circular means don’t work exactly like that, but still it should be roughly the second bearing divided by 3.
Here is a graph of comparing the circular mean against the naive mean in this case, with the second bearing angle plotted on the horizontal axis:
You can see the nonlinearity in the circular mean, but whatever, it’s pretty close, that’s the price you pay for using a mean that doesn’t behave stupidly when values cross between 000° and 360°.
Now here’s the same graph with the eigenvector-based mean as well:
Oops. It’s very good at small angles! My intuition wasn’t completely stupid! But as the bearing of the second angle approaches 090°, the dominant eigenvector of the covariance matrix of the coordinates starts to point back towards 000°. This is the surprising eigenvector of the title. What’s going on?
I hinted very briefly at the problem earlier: it’s related to the eigenvector minimising a sum of squares, whereas averaging is typically a linear operation.
If you rotate the point (1, 0) or (-1, 0) a few degrees, the X-coordinate doesn’t change much: the point is travelling along the unit circle, and the unit circle is vertical at (±1, 0). But a point further around the circle will have its X-coordinate change a bit if you rotate a few degrees. This means that if you were trying to maximise the variance of the transformed X-coordinate by hand, you could try the following procedure:
Rotate so that the pair-of-points with greatest weight are at (1, 0) and (-1, 0).
Rotate a few degrees to get the other pair-of-points a bit closer to the X’-axis.
In the second step, you don’t reduce by much the contribution to the variance of the pair-of-points with greatest weight, but you do increase the contribution from the other pair-of-points.
But if the naive average requires rotating quite a lot of degrees in the second step, then the pair-of-points with the greatest weight starts moving too far away from (±1, 0), and its contribution to the variance will start being reduced more rapidly, especially so because the coordinate is being squared. But this is the pair-of-points with the greatest weight! It’s not a good trade-off to do this second rotation. So the eigenvector starts to point back to where that pair-of-points started.
That’s how the maths works out, anyway. I certainly didn’t guess it ahead of time, and my wordy explanation in the previous paragraphs probably wouldn’t have convinced past-me before I actually tested it.
Anyway, my accumulated knowledge about eigenvectors is not all wasted: the dominant eigenvector can still be used to define a reference half-plane, and I can calculate a circular mean of the points in my pairs-of-points that are in this half-plane.





