GPT versus one-node Leela
Doubling as an introduction to chess engines
I am rated 1800 FIDE, 1900 Lichess blitz. I have never done anything in computer chess. While I think the gist of my explanations is correct, imprecisions are likely, and I am certainly omitting many technical details.
OpenAI has released many large language models. One of them, gpt-3.5-turbo-instruct, can play chess to a decent level out of the box, with no fine-tuning required: you prompt it with the start of a chess game, and it usually continues it with a valid move.1
I think that for chess players, the best way to get a sense of GPT’s chess skill is to play against it; the second of those linked videos shows me losing a blitz match 8-2. But games against other engines may also be of interest, and one in particular has intrigued me for a while.
Leela2 is a neural-network-based chess engine, an open-source descendant of AlphaZero. A bit over a year ago, I wrote:3
An interesting experiment that I probably won’t do, but would find interesting if I did: creating games between GPT and an old version of Leela running on one node, … without any searching. That would be a fair fight, with both engines using only “instinct”. Leela should usually win, but I think the score would be less than 100% with an older, weaker Leela.
Well I’ve had a nice long summer holiday this year, and now I’ve run that experiment, with 100-game matches against various Leela networks with moves selected from one-node calculations. GPT wins some games, even a win and a few draws against the biggest Leela network! GPT scores 21.5/100 against the network that first took Leela into the Premier Division of the Top Chess Engine Championship.
As I started to write up these results and interpret them, I realised that I understood very little about chess engines in general and Leela in particular. This post therefore presents a lot of background before getting to the matches that are the post’s nominal purpose.
I imagine this post having two readers (which is below average). One is a chess player who will be interested to learn about the mechanics of different chess engines in Section 1. The other is interested in AI, and would like to have some more data points about the gpt-3.5-turbo-instruct model’s chess strength. Section 2 presents some Leela history to provide context for my GPT versus one-node Leela matches, and Section 3 contains the description and results of those matches.
I’ve written the early part of Section 1 without getting too technical; once the algebraic chess notation hits, you can safely skip forward if you don’t understand it.
1. A long introduction to computer chess
A popular one-sentence summary of Kasparov’s loss to Deep Blue in 1997 might be, “Deep Blue won by analysing hundreds of millions of moves every second, allowing it to look many moves ahead.” But such a description hides several different aspects of a chess engine:
How should it search those millions of positions every second? The number of possible future positions from a current board state can increase extremely rapidly, preventing an exhaustive search through all of them. If both players each have about 20 legal moves on each turn – often there would be much more than 20 – then looking even five moves ahead in a completely systematic fashion would require processing about 10 trillion positions, which is too much. When there are lots of pieces on the board, chess is too complicated for a brute-force search.4
Given a position, the engine has to estimate an evaluation: is it equal, better for White, or better for Black? How much better? Internally these “evals” might be in the form of probabilities of win, draw, and loss; or they might be in the form used for human consumption, which is units of pawns.5 An eval of +1 is a position where White has an advantage equivalent to playing with an extra pawn; an eval of +0.3 is a small edge; -2 is like Black having won a rook for a knight, or having two extra pawns; 0.00 is equal.
(A separate scale is used when the computer finds that there is a forced checkmate.)The nitty gritty programming to optimise the calculation so that moar millions of variations can be analysed every second; not the subject of this post.
For computer chess competition – games between engines – clock management also plays a role, as it does in human play. The players start with some amount of time to make all their moves (often with a small increment added each move), and have to spend that time appropriately, not wasting time on easy moves, so that they can have a long think when the position calls for it. Engine clock management is of almost no interest to me.6
The first two of those bullet points are the focus of this section. They illustrate fundamental changes in the chess engine world since the neural network revolution that was announced in 2017 when AlphaZero defeated the reigning computer champion Stockfish 8. I find it useful to think of three different engine types:
Old Stockfish (versions up to 11): These classical engines were entirely human-coded, both the search and evaluation.
AlphaZero/Leela: Engines based on AlphaZero ideas use neural networks to do the evaluation and to guide the search, though the scaffolding for the search is still human-coded.
Modern Stockfish (versions 12+): Stockfish today retains human-written search, but uses a neural network for the evaluation.
The next two subsections talk about evaluation and search from a classical, old-Stockfish perspective. I’ve put the evaluation first because the search will be affected by the evaluations it finds.
Evals
A human-coded evaluation function might start with a material count: 1 point for a pawn, 3 for a knight or bishop, 5 for a rook, 9 for a queen. Whichever side has the most points is deemed to be winning by that margin. Even this simple counting system, combined with state-of-the-art searching through the tree of variations, is sufficient to create an engine that beats club-level human players. The simpleEval Lichess bot uses an old Stockfish engine whose evaluation function is replaced by a 1-3-3-5-9 material count plus a small random number,7 and it is rated in the high 2200’s in Lichess blitz (top 2.5% of the Lichess blitz population) and bullet (top 5%).8
As someone who is not particularly close to the high 2200’s, it is infuriating to play against simpleEval: it makes the dumbest, most useless moves imaginable, until you make one little slip-up and then it pounces with superhuman precision to win a pawn, and eventually the game.
But simpleEval is not at the level of a grandmaster. Analysing millions of variations on its own is not enough to be better than the best humans: the evaluation function needs to be more sophisticated. If a bishop is currently blocked behind its own pawns on the same coloured squares, then perhaps it’s only worth 2.6 pawns instead of 3. If Black has castled kingside, then a white knight on f5 might be worth 4 pawns instead of 3 (Kasparov).9 A vulnerable king might more than offset an extra piece. Pawns themselves change in value based on their structure and how close they are to promotion.
Programmers of engines like old Stockfish would write many, many such rules into its evaluation function, perhaps guided by a human master’s advice, or through experiment with engine-versus-engine games. Browsing the comments in Stockfish 11’s evaluate.cpp shows some examples. A selection from the function handling piece values: Bonus if [bishop or knight] is on an outpost square or can reach one; Bonus for bishop on a long diagonal which can "see" both center squares; Bonus for rook on an open or semi-open file; Penalty when [rook] trapped by the king, even more if the king cannot castle; Penalty if any relative pin or discovered attack against the queen.
Different functions in the same file handle space, threats, initiative, king safety, passed pawns, etc. (Pawn structure gets its own file.) Space is defined as the number of safe squares available for minor pieces on the central four files on ranks 2--4. Safe squares one, two or three squares behind a friendly pawn are counted twice. The count is then multiplied by a weight that scales as the square of the number of pieces the player has. To me it feels a little alien to reduce the concept of space to such formulas, but of course some sort of arithmetical proxy is needed for a hand-coded engine to take the concept into account.10
Searching
Even hundreds of millions of positions is a small fraction of the total possibilities over the next dozen half-moves from a position with many pieces on the board. The engine has to discard unimportant variations early – if a move leads to the loss of a piece, then there is probably no need to search further. You want the engine to spend time going deeper on the critical variations, where both players are making the best moves. But sometimes the best move is to sacrifice material for later gain, and it is important that the engine doesn’t always terminate the analysis of such moves early.
Wikipedia tells us that Stockfish “uses a tree-search algorithm based on alpha–beta search with several hand-designed heuristics”. In their original formulation, alpha and beta nominally represent hard bounds on the eval. Suppose that alpha = 0.3 and beta = 1.4. If in one of the variations analysed, an eval for White of 2.1 is found, then that (sub)variation can be discarded: Black would not enter it, instead playing a different earlier move that keeps the eval below 1.4.
In reality the bounds are not hard, and after a few iterations, old Stockfish sets an aggressively narrow [alpha, beta] “aspiration window” based on the eval it’s found so far. This means that more of the search tree is discarded in favour of deeper analysis on the lines likely to be critical. But it is possible that the search finds an eval outside the aspiration window, failing low or high, and then it has to update the window and start the whole search over again – maybe some of the earlier moves had been too quickly discarded. The appropriate balance between these competing possibilities is determined empirically: the best window size is whatever makes the engine win more games.
As for the heuristics, a look through the code reveals plenty of them, with informative comments saying how many Elo points each is worth. Futility pruning: child node (~50 Elo); Null move search with verification search (~40 Elo); ProbCut (~10 Elo); Pruning at shallow depth (~200 Elo); Countermoves based pruning (~20 Elo); Futility pruning: parent node (~5 Elo); Prune moves with negative SEE (~20 Elo); else if (!pos.see_ge(move, Value(-194) * depth)) continue; // (~25 Elo); Extensions (~75 Elo); Reduced depth search (LMR, ~200 Elo).
There are potential failure modes that need guarding against when writing a search algorithm. The main search might reach a position where an equal exchange of pieces has been started but not completed, for example if White has just taken Black’s queen, and Black will capture White’s queen only on the next move. An evaluation that sees White having an extra queen in such a position might erroneously give White a completely winning advantage. Stockfish does a “quiescence search” at the end of its main search to ensure that the position that gets evaluated is “quiet”, with no free pieces available for capturing.11
The order in which possible moves are analysed is also important for efficiency. You don’t want the engine to start by going deeply into a quiet line when there are tactics elsewhere that could win or lose the game in the next couple of moves. It is probably best to start with the traditional “forcing moves” of checks, captures, and threats. But usually when you capture a defended piece with a piece of greater value, you simply lose material. Stockfish puts such likely-bad captures at the end of its order of moves to analyse.
To get a feel for how old Stockfish approaches a position, I decided to study one tactical example quite closely. I’ve put it in its own particularly technical subsubsection, which you can safely skip.
A particularly technical subsubsection: Stockfish 11 search example
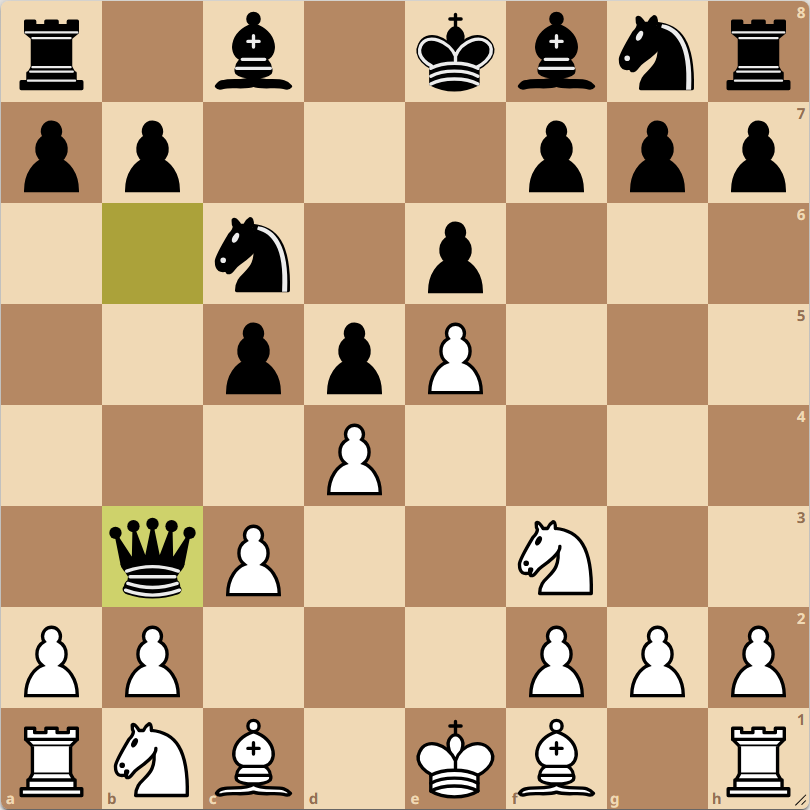
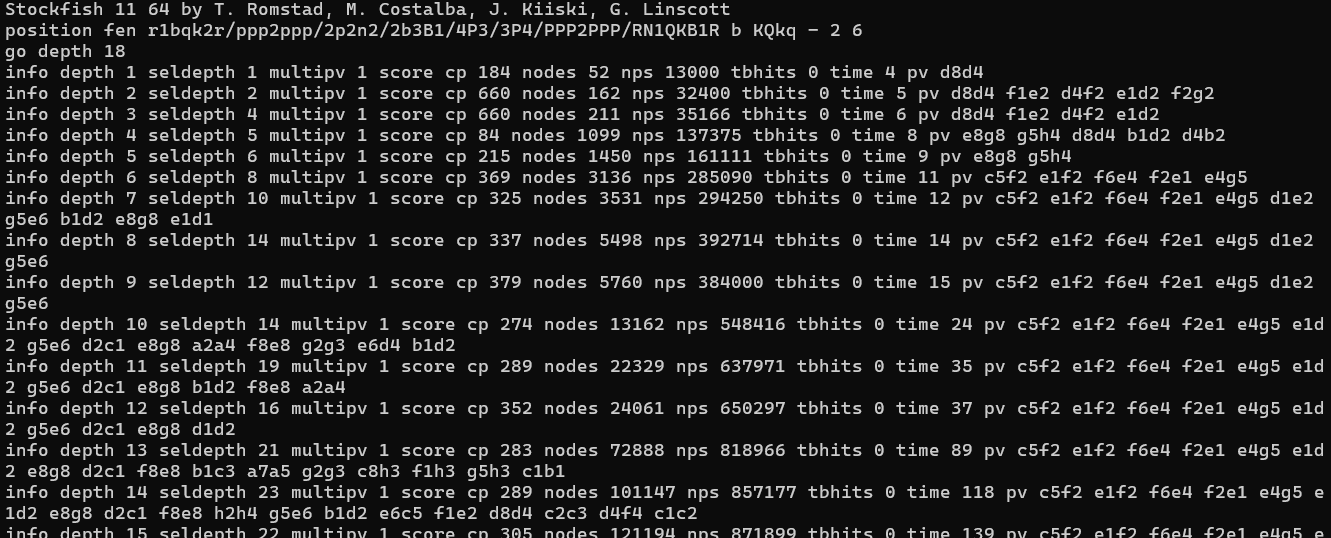
Consider the following Stafford Gambit position, in which White has fallen into the 6.♗g5?? trap.
Black is better after 6…♕d4, threatening mate and b2, but there are two stronger moves. One is 6…♗×f2+! 7.♔×f2 ♘×e4+ forking king and bishop, which recovers the gambited pawn, wins another, and leaves White without castling rights. The line would end after five half-moves with the capture of the bishop. But the strongest move is 6…♘×e4!!, when White’s best is to decline the queen sacrifice, the principal variation being 7.♗e3 ♗×e3 8.f×e3 ♕h4+ 9.g3 ♘×g3 10.h×g3 ♕×h1 and Black is up an exchange and pawn.
The latter line is nine half-moves long. Stockfish uses “iterative deepening”, starting with a depth=1 search before going to depth=2, then depth=3, etc., the results from each depth initialising the search parameters at the next. Based on the lengths of the lines above, we might therefore expect …♕d4 found first, then …♗×f2+ at depth=5, and finally …♘×e4 when it reaches depth=9. Here are the results:12
Depth Eval Move
1 -1.84 ♕d4
2 -6.60 ♕d4
3 -6.60 ♕d4
4 -0.84 O-O
5 -2.15 O-O
6 -3.69 ♗×f2+
7 -3.25 ♗×f2+
8 -3.37 ♗×f2+
9 -3.79 ♗×f2+
10 -2.74 ♗×f2+
11 -2.89 ♗×f2+
12 -3.52 ♗×f2+
13 -2.83 ♗×f2+
14 -2.89 ♗×f2+
15 -3.05 ♗×f2+
16 -3.04 ♗×f2+
17 -3.61 ♘×e4
18 -4.27 ♘×e4It finds the bishop sacrifice at a depth of 6, pretty close to the five half-moves counted earlier. But the sacrifice on e4, despite apparently needing a depth of only 9, is not returned as the leading move until depth 17. What’s going on?
One thing that’s going on is that my results above used the command-line default of calculating only one principal variation. When you use Stockfish to analyse, you almost certainly have it set to three or more. The required depth for it to find …♘×e4 is much shallower if a high MultiPV value is set. This forces the engine to calculate a line for each move rather than ending the analysis early when one of its heuristics tells it to stop. When it does the fuller calculation, it re-evaluates the move and in this case it finds 6…♘×e4 best at a depth of only 12.
But the original set of results, without MultiPV and requiring depth=17, are still to explain. To investigate, I built Stockfish from source and added lots and lots of debug logging to the search.cpp file, giving me 200MB of logs to sift through.13 The short answer is that …♘×e4 is initially given very low priority in the search (because it looks like a bad capture), and Stockfish often reduces the depth to which it searches the low-priority moves (late-move reduction; LMR).
Now for a longer answer. At depth=1, the initial order of moves to test has the two sacrifices very close to the end; only the blunder …♕×d3 is given lower priority. This part of the code looks at “static exchange evaluations”, in which you count material that gets traded on the same square. It is usually a bad move to capture a defended pawn with a piece, so the starting assumption is that …♘×e4 and …♗×f2+ are not good.
The spike in the evaluation for 6…♕d4 at depths of 2 and 3 is because of another move-ordering “mishap”. The best defences against the mate on f2, namely 7.♗h4 and 7.♗e3, happen to be late in the move order. The engine will continue systematically searching if it doesn’t find a defence against mate, but after analysing 18 useless moves, it finds that 7. ♗e2 is “only” -6.61. Shortly afterwards, futility-pruning kicks in – if it has already searched a number of moves greater than a threshold that is dependent on the depth remaining, and it is not getting mated, then it doesn’t analyse any more replies.
At depth=3 some other pruning heuristic kicks in early (countermoves; I haven’t studied this one); at depth=4, the search gets to 7.♗e3 (it seems to have been brought forward in the move order, perhaps because the engine bumped down all the moves that allowed the mate; also the futility threshold would be higher by now and more moves analysed regardless) and the evaluation returns to something roughly appropriate for 6…♕d4.14
At depth=5, seemingly enough to find the sacrifice on f2, the eval for castling, which is the expected best move, is higher than expected, outside the aspiration window. The search is terminated early with a fail-high and restarted at a depth of 4, then 3, then 2, and finally 1 before it analyses 6…♗×f2+, now at insufficient depth. I do not know why the depth is globally reduced in this way.
At depth=6 this global reduction of depth does not occur before the bishop sacrifice is analysed and found to be good, and it becomes the leading move.
By depth=9, we naively expect that the sacrifice on e4 to be found as best. But moves late in the move order are considered unlikely to be good, and rather than wasting time analysing them deeply, they are analysed at reduced depth as long as they satisfy various criteria. The depth of 9 is globally reduced to 6 after some fails, and a reduced depth of just 2 is used for …♘×e4 specifically.
At depth=10, the reduced depth of 6 is actually sufficient for Stockfish to evaluate …♘×e4 positively (i.e. in favour of Black), but its eval doesn’t take it ahead of …♗×f2+, and the vagaries of the LMR reduce it to 5 half-moves and an early futility-prune at depth=11 and depth=12.
At depth=13, the reduced depth is 8, and the eval for …♘xe4 gets close to that of …♗×f2+. It gets a reduced depth of 9 and a pretty long analysis at depth=16, and finally a full-depth analysis at depth=17 and promotion to the principal variation.
One question I had is why …♘xe4 keeps getting subjected to LMR while …♗×f2+ is fully analysed at depth=6. The answer lies in one of the (many) conditions to do the LMR. At the start of the search, a “static evaluation” of the position is calculated – what the eval would be if there were no further searching. If the material value of a captured piece plus the static eval is greater than the current alpha, then the LMR will not be performed: it is plausible that the capture will improve the eval, so it is analysed to full depth (possibly still to get pruned one level deeper than previously).
When …♗×f2+ is tested at depth=6 for LMR, the alpha is based on the eval after castling, and an extra pawn would be an improvement over that. However, once …♗×f2+ is analysed deeply, the eval and hence alpha value increases substantially – the position is better for Black by more than two pawns’ worth. The material value of the e4 pawn on its own would not be sufficient to take the static eval past the new, larger alpha, so …♘×e4 continues getting LMR’d until eventually even the reduced depth is sufficient for the line to be properly analysed.
I am satisfied enough by this explanation.1516
AlphaZero/Leela
The one-sentence summary of AlphaZero is that it replaced the human-written engine with a neural network trained by self-play – 44 million games played against itself, according to the appendix of the arXiv paper. But even ignoring all the complexity and thought that needed to go into designing the network architecture, the simple summary hides some high-level implementation details.
(I know this because when I started drafting this post, I had a clear idea in mind as to how to interpret my experiments with games between Leela and GPT. As I checked various references to make my arguments precise, I realised that my whole conception of neural-network-based chess engines was wrong!)
The network contains many layers, with the final outputs split across two “heads”:
the value head gives the evaluation;
the policy head calculates a “probability” for each legal move; these probabilities initialise a tree search algorithm. I’ll refer to these interchangeably as “policy probabilities” or “policy priors”.17
The two heads are built on the same underlying network, so the network is trained for both outputs simultaneously. The value head is conceptually straightforward: you want the evaluation of a position to predict the outcome of a game played from that position.
The policy head is subtler. The self-play training games work by selecting each move by an algorithm called Predictor + Upper Confidence Bound for Trees (PUCT).
(The algorithm is frequently referred to as Monte Carlo tree search, including by the authors of the AlphaZero paper. I find this terminology confusing, since processes called ‘Monte Carlo’ would typically be based on simulations involving random numbers. Randomness can be introduced into PUCT, but the search can also be implemented purely deterministically.)
Selecting a move by PUCT search
Each iteration of the PUCT goes at most one single (half-)move beyond what has previously been searched. For example, from the starting position, the search may go like this:18
1.♘f3
1.♘f3 d5
1.♘f3 d5 2.d4
1.c4
1.c4 e5
1.♘f3 d5 2.d4 ♘f6
1.g3
1.g3 e6
1.d4
1.d4 ♘f6
1.♘f3 d5 2.g3
And so on.19 (The network that I used for this example was not a fan of 1.e4!)
Each iteration of the search starts at the current game position. The next PUCT move chosen is the one which maximises a score function, which for a newly-encountered position is equal to the policy prior. Whenever it chooses a move that it hasn’t chosen before, it evaluates the new position using the network’s value head. This evaluation is then propagated back along all the moves that led to that new position, updating the score function for each move in the line. A move’s score function becomes a blend of its policy prior and the average of the evaluations calculated at the end of lines containing that move. The search then returns to the current game position for the next iteration.
Let
P(a) be the policy probability for move a,
Q(a) be the average evaluation calculated at the end of lines containing move a (this is zero if the move hasn’t been chosen yet),
N_total be the number of search iterations so far from the position where move a can be played,
N_a be the number of times move a has been chosen so far, and
c be a hyperparameter set by humans (usually to around 2.5 or 3) that controls the relative importance of the policy prior P versus the observed evaluations Q.
The score function is then
The division by N_a + 1 and the multiplication by sqrt(N_total + 1) mean that the search will eventually look at moves other than top policy move, as long those other moves have P > 0.20 Another tendency is that for the frequently-chosen moves, as the number of iterations increases, the relative importance of the observed evaluations Q increases, so that moves which lead to good results will tend to be chosen more often.
(The literature usually calls these search iterations playouts. I have avoided this term because it misled me into thinking that each playout would go until the end of the game, or to some specified depth. But the first play“out” is only ever one move long!)
During AlphaZero’s fast self-play training games, it would do 800 PUCT iterations at each move; many more might be needed to find an unlikely-looking sacrifice while analysing. At the end of the search, each legal move from the current game position will have been chosen some number of times. Dividing these counts by the total number of iterations (800) defines a new set of probabilities for the legal moves; the network is trained to minimise the difference between the policy probabilities and these new post-search probabilities.
To choose the move in a training game, there are two natural approaches:
Select the move which was chosen most often during the PUCT search;
Make a random choice according to the post-search probabilities.
Making the random choice means that the network will learn to process positions that result from bad moves as well as good ones, but the risk is that the evaluations become slightly scrambled – the network might “learn” that a position is bad because a randomly-chosen move later in the game was a losing blunder, when objectively the position was good. So there is a balance to be struck here, and apparently the randomness is switched off after fifteen moves.
When you’re using Leela as a chess engine to analyse, or it is playing a competitive game, the default settings ensure that it always chooses the move that was visited most often. However, by default a small amount of randomness is introduced, so that it doesn’t always play the same moves, by adding some noise to the policy priors.
Back to the policy head discussion
The policy head is trained to output a set of probabilities that (hopefully) matches those generated by a PUCT search. This is not the same thing as the real-world probability of each corresponding move being played. For example, consider the following position, in which Black has just captured White’s queen on b3:
There is only one sensible move for White in response, which is to recapture Black’s queen with the a-pawn. This position has occurred almost 200,000 times on Lichess, and across all rating levels and time controls, 99.88% of White’s moves are taking the queen. Most of the other 0.12% are mouse slips, moving the a-pawn forward one square but not moving the mouse to the right enough to get the pawn over the b3 square.
When I give this position to the biggest Leela network (the big transformer BT4-spsa-1740, “currently being sent to engine competitions”), it assigns a “probability” of only 82.6% to taking the queen. It gives 1.1% “probability” to the other two moves by the a-pawn, and at least 0.5% to all other moves (least “probable” being Bb5).21
The logic here is that sometimes the obvious move won’t be the best one, and the best play will emerge when the PUCT search gets to explore, at least a little bit, some of the less likely moves. The network therefore trains to give probabilities that allow for some exploration. In the above case, the search will quickly confirm that taking the queen is the only sensible move. There is little or no benefit to having the network assign a higher probability than it already does.2223
Perhaps it is of interest to test the policy probabilities against a more difficult tactical position. Here it is White to play, and there are two obvious candidate knight jumps, to f5 and h5: both threaten mate on g7 while discovering an attack by the rook on Black’s queen.

But only one of the two moves leads to White emerging with the advantage, and it is too difficult for me to work out at a glance which one is correct (puzzles at this difficulty level usually take me several minutes). The big transformer gives the correct knight jump a policy probability of 57.9% and the wrong knight jump 20.9%. For one of the smaller networks on Leela’s bestnets page,24 the probabilities are 48.8% and 24.3%. An old network from July 2018 (id10161) gives almost equal policy priors, 27.1% for the correct one and 27.7% for the wrong one.25
Leela search example
Let’s look at the same Stafford Gambit position whose old Stockfish search analysis was described earlier.
A Leela network from August 2018 (id11248) gives policy priors of 41.5% for 6…♗×f2+, 22.0% for 6…♕d4, 12.0% for 6…h6, and just 7.1% for …♘×e4, the best move.26
Once each of those moves is on the board, the network’s value head assesses the first two options (…♗×f2+ and …♕d4) as good for Black, especially the sacrifice on f2, and the other two as good for White. I will present evaluations as they are in my debug logs, which are on a scale of -1 (certain loss for the player making the move, which is Black) to +1 (certain victory). The bishop sacrifice is at 0.31, while …♘×e4 is at -0.07.27
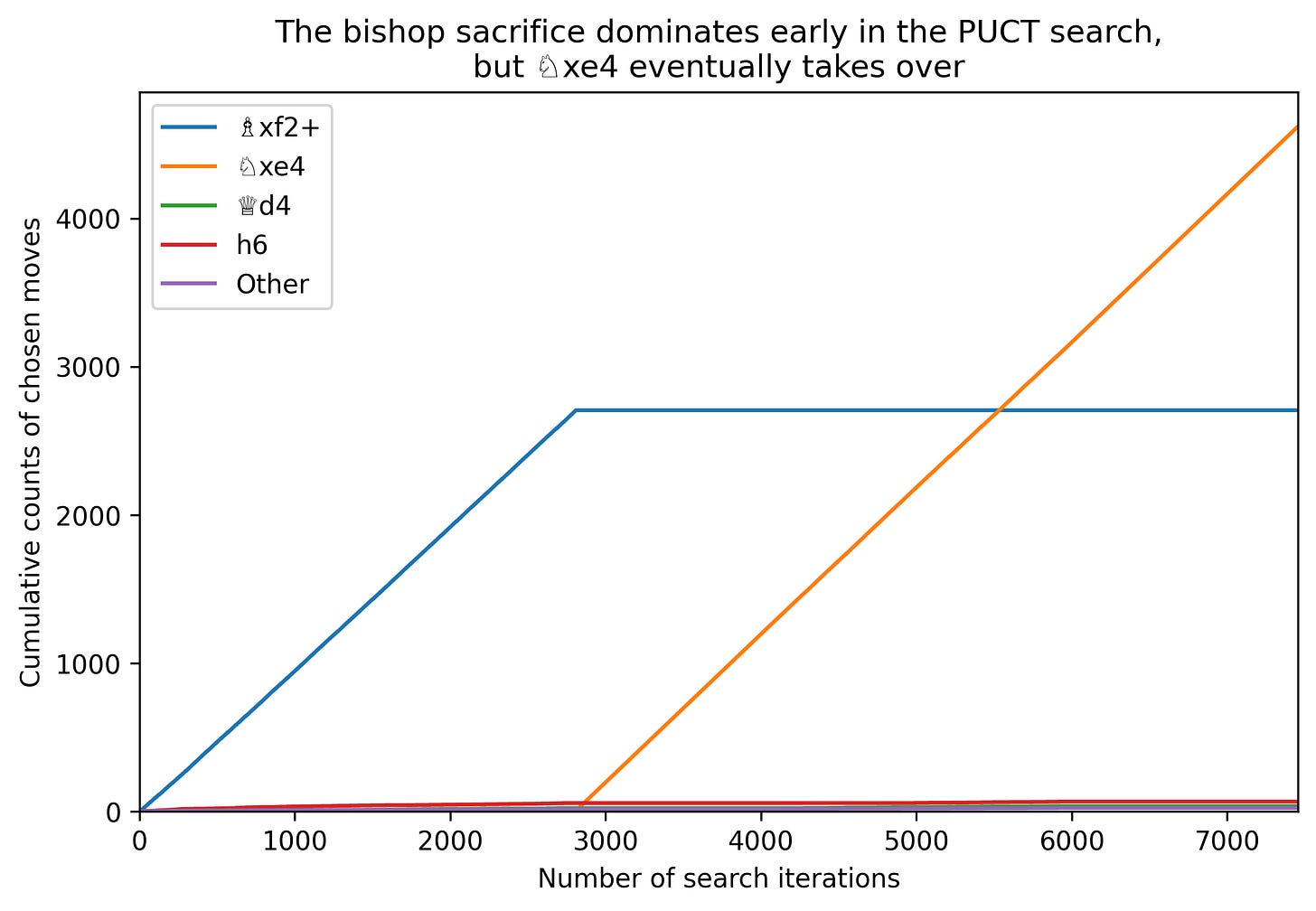
Most of the early PUCT iterations therefore choose …♗×f2+, which appears best on both policy and evaluation. It first looks at 6…♘×e4 on iteration 22, where its negative evaluation keeps its score function below that of …♗×f2+.
On iteration 127, it looks at 6…♘×e4 7.♗×d8 and evaluates the position as -0.78, very likely a win to White because Black just lost their queen. The Q value for …♘×e4 gets even worse compared to …♗×f2+, and the move doesn’t get chosen again for hundreds of iterations.
On iteration 566, it chooses 6…♘×e4 7.♗×d8 ♘×f2 (wrong capture!) and evaluates it as -0.79.
On iteration 1154, it chooses 6…♘×e4 7.♗×d8 ♘×f2 8.♕e2 and evaluates it as -0.84.
On iteration 1878, it chooses the correct follow-up, 6…♘×e4 7.♗×d8 ♗×f2+ and evaluates it as -0.35 – better than it was, but not enough to displace 6…♗×f2+.
On iteration 2334, it gets to 6…♘×e4 7.♗×d8 ♗×f2+ 8.♔e2 and evaluates this mate-in-one position as a likely loss, -0.40. (By contrast, the big transformer BT4 sees it as an overwhelmingly likely win.)
Finally on iteration 2810, it reaches 6…♘×e4 7.♗×d8 ♗×f2+ 8.♔e2 ♗g4#, checkmate delivering a certain victory and therefore an evaluation of +1.00. From then on the algorithm overwhelmingly chooses 6…♘×e4. Here is a graph:
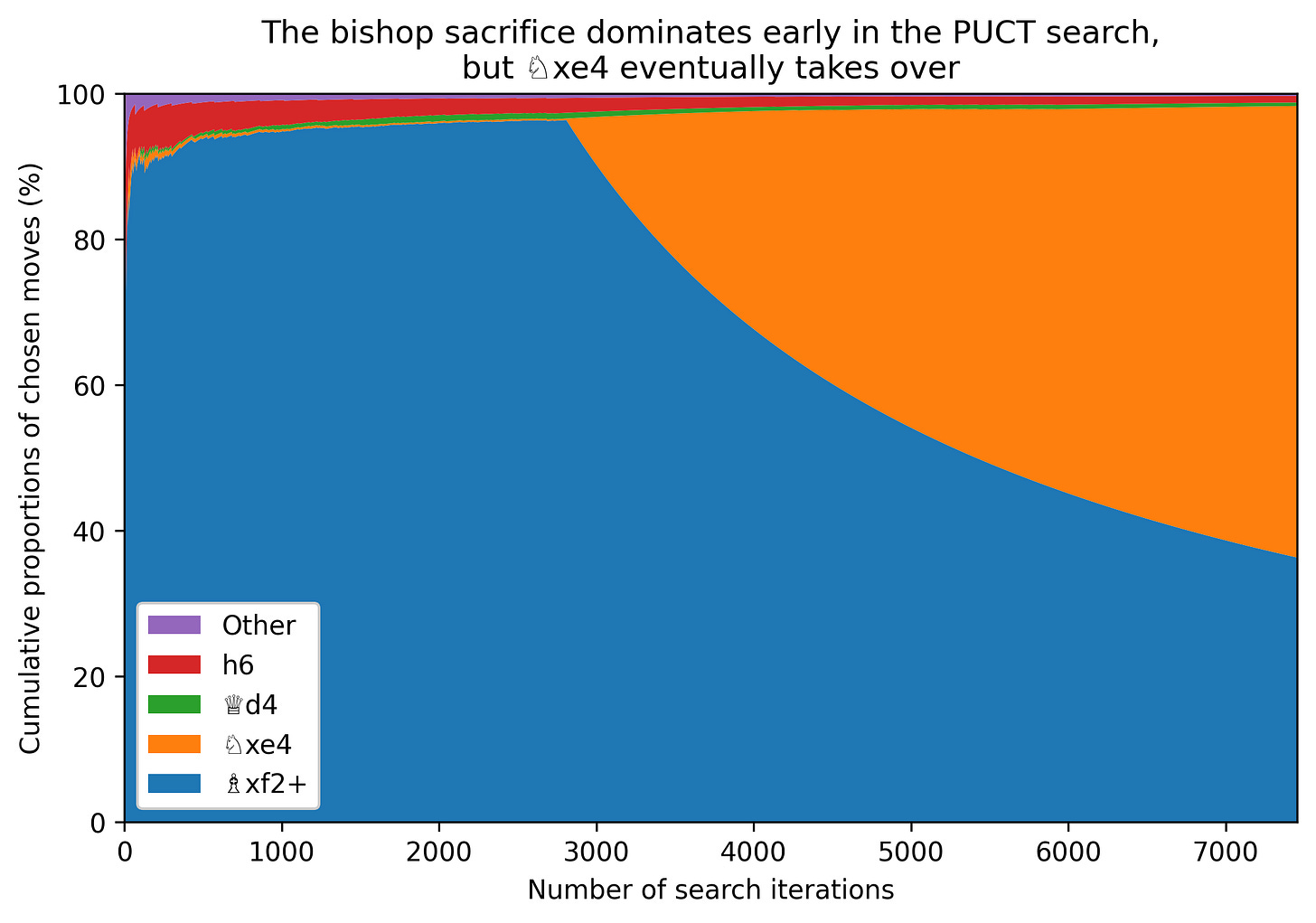
The graph of the cumulative shares looks prettier, and shows a little more detail on the frequency of the other move choices. But it obscures the fundamental dynamic of how it’s overwhelmingly one move or the other that’s trialled at different times in the search from this position:
(In the 7456 iterations from this example, all moves except 6…♘g8 and 6…♗a3 were chosen at least once, though most moves were only chosen once.)
Of some practical importance is that you need good hardware (GPU processing) for Leela’s searching to be efficient compared to Stockfish. On my rubbish CPU-only laptop, it takes more than two minutes for the above search to start returning 6…♘×e4, compared to 0.23 seconds for Stockfish 11 and 0.026 seconds for Stockfish 17.
The end of the Leela subsection
A long time ago, I started this post by wanting to set up matches between GPT and one-node Leela. We’re now able to understand what this means. If Leela only processes one node, that means it looks only at the current position (a node), outputting the policy probabilities; the move with the highest probability will be played. There will be no search, which would require more nodes to be processed. This is loosely analogous to a GPT text completion, which likewise doesn’t do any search, instead simply outputting whatever text – usually a chess move – that the LLM calculates as most likely to follow after a numbered list of all the previous moves in a game.
But before we get to the matches, I’ll go over some Leela history, since most of my matches are against older networks.
2. The neural network era
The initial AlphaZero arXiv paper described it defeating Stockfish 8 by a margin of 64-36. Initial reaction from chess engine programmers who posted on forums was sceptical, by which I mean there were a lot of sour grapes. Complaints about unequal hardware, the wrong hash size allocated to Stockfish, a time control that handicapped Stockfish, etc.
Whatever validity some of these gripes had, subsequent years have been a complete vindication of the neural network approach. DeepMind did not publicly release AlphaZero, but their publications gave enough information for people to start training Leela as a distributed-computing open-source quasi-clone.
Training on Leela started in early 2018, initially with a smaller network than AlphaZero’s. I will not pretend to understand the network architecture (originally based on convolutional neural networks), but I’ll follow the shorthand notation of 6 × 64 to denote 6 “blocks” of 64 “filters”; as I understand it, AlphaZero was 19 × 256.
DeepMind had enormous TPU resources available to it from Google, allowing the eye-popping headlines of surpassing Stockfish in just hours of training through lots of parallel processing. By contrast, the early Leela effort was designed to allow CPU-based training, and the people organising it did not have the ambition to immediately surpass AlphaZero.
The first network of the “old main” Leela line was uploaded on 20 February 2018; the network files themselves from that era have disappeared, as far as I can tell, but the list is available on the Wayback Machine. I used to assume that there was one canonical Leela network, which slowly improved with more and more training over the years, but the Leela devs have often split the training into different concurrent runs, trialling different network architectures and learning hyperparameters, sometimes doing a full reset to random weights.28 In April 2018, they increased the network size to 10 × 128, just in time for Leela’s first entry into the Top Chess Engine Championship (TCEC).
Network ID123 was the first at the increased size; ID125 was used29 for Leela’s TCEC debut, as it competed in season 12’s fourth division (the lowest), scoring two draws, 25 losses, and one forfeit win when its opponent crashed. It would be fun to play against this network! But I can’t find the weights.
On 15 June 2018, the Leela team started a fresh training run with a new numbering system, still in use today with the full archive of network snapshots available for download.30 (To see the earliest networks on that page, you’ll have to scroll to the bottom and click the “warning: large page” link; Chrome eats gigabytes of RAM in displaying the table.) The old run continued in parallel until August, the best network being ID595, 15 × 192.
After some fits and starts – training runs abandoned early for various reasons – test run 10 began on 28 June, with 5-digit network ID’s that began with ‘10’ and eventually ‘11’ as the training continued on the 20 × 256 network.
Test10 is of most interest for my GPT comparisons, it being the earliest really successful Leela run that I have access to. The fourth division of TCEC’s season 13 started in August, with network 10161 taking Leela to a win with a score of 20/28 and promotion to the third division.
Network 10520 was substituted in for the third division, where Leela finished in a disappointing tie for second. Chat in the Discord server at the time suggests that it played about 200 Elo points below expected (e.g. scoring 50% against opponents they’d had expected to score 75% against), and a page on the Leela wiki talks about hardware issues with the TCEC server and some poor time management settings.
The big issues were all fixed in TCEC season 14, whose third division started in December 2018. With network 11248, Leela won the third division, then the second division, then the first division, being promoted to Premier.
The question then was whether to continue using 11248 or swap in a network from the more recent test30 training run. “consensus appears to be that we're bored enough with 11248 to be willing to risk it,” says an amusing Discord message. Running with network 32194, Leela tied for second with Komodo (24/42) behind Stockfish (29/42) in the Premier division. Due to boring reasons (a countback after another engine was disqualified for too many disconnections), Leela qualified ahead of Komodo for the 100-game superfinal against Stockfish 10 in February 2019.
With network 32930, benefiting from an extra month of training compared to 32194, Leela lost its first superfinal by just 49.5-50.5. The two engines traded the next few superfinals, Leela winning seasons 15 (May 2019) and 17 (April 2020), and Stockfish winning seasons 16 (Sep-Oct 2019) and 18 (June-July 2020).
Stockfish 11 was the last Stockfish to use a classical, human-coded evaluation function.31 Stockfish 12, used in TCEC season 19, incorporated its own neural network for evaluation, while continuing to use human-coded move-ordering and alpha-beta search. Stockfish has won every TCEC season since, Leela usually in second place.
3. GPT versus Leela one-node
The training data for the GPT models includes an enormous amount of text from the Internet, and some of that text is chess games in PGN format: millions and millions of games containing headers with metadata and numbered moves listed in algebraic notation. The transformer networks are large enough to learn the patterns of those chess symbols and are capable of continuing the text of a PGN file with sensible, decently strong moves even in positions never seen before.
OpenAI want people to use their ‘chat’-style API’s and interfaces, but for continuing a PGN file, it is easiest to use the old-style ‘completion’ API, asking for a small number of tokens to be returned, enough for a move. I make up some PGN headers (a Carlsen-Caruana game), start the moves with “1.” if GPT is playing White, or one-node Leela’s move if Leela has White. As the game progresses, all previous moves become part of the prompt.
Each of my matches against a Leela network consists of 100 games. Openings are from every tenth ECO code: A09, A19, A29, …, E99. This should give a decent selection of openings that were popular when the ECO codes were created in the 1960’s, when chess was good. Each opening is used for two games, reversing the colours for the second game.
A hundred games costs about US$1.50 in OpenAI API usage. A match lasts about an hour if not parallelised, and I stay at about 10% of gpt-3.5-turbo-instruct’s rate limit of 90,000 tokens per minute. A Python script to run a match is on Github.
Some miscellaneous match details:
Early Leela could be very inefficient at finishing off easily won endgames (e.g. if it was up a rook and queen, any move would maintain an evaluated probability of victory of 1, and instead of winning quickly it might shuffle its pieces around for a while). I am not interested in seeing this, so I adjudicate a game as a win for Leela if it has maintained a material advantage of at least 5 points for 10 consecutive half-moves.
I am interested in GPT’s ability to close out endgames, so I do not make any such adjudications when GPT is material up.
A game is declared drawn when either player can claim a draw, effectively implementing an automatic “2.5-fold” repetition rule. This is slightly inelegant (perhaps an engine would want to deviate rather than making the position appear for a third time), but it makes the coding easier because I can use the Python chess library’s
Board.outcome(claim_draw = True)without having to count repetitions myself.The GPT text completion may not be a legal move.32 Most of the time, I try again, giving it five attempts to complete a legal move (if GPT is running at zero temperature, I increase the temperature to 1 for these attempts, to allow for some variation). The game is declared won to Leela if none of the five completions is a legal move.
There are a couple of minor cases. Non-ASCII characters are stripped, as are leading dots, which happen occasionally (e.g. in a prompt ending “24.”, the completion might be “.Qc4”, duplicating the dot that follows the number), prior to checking if the text is a legal move.
Results
PGN files for all matches are on Google Drive.
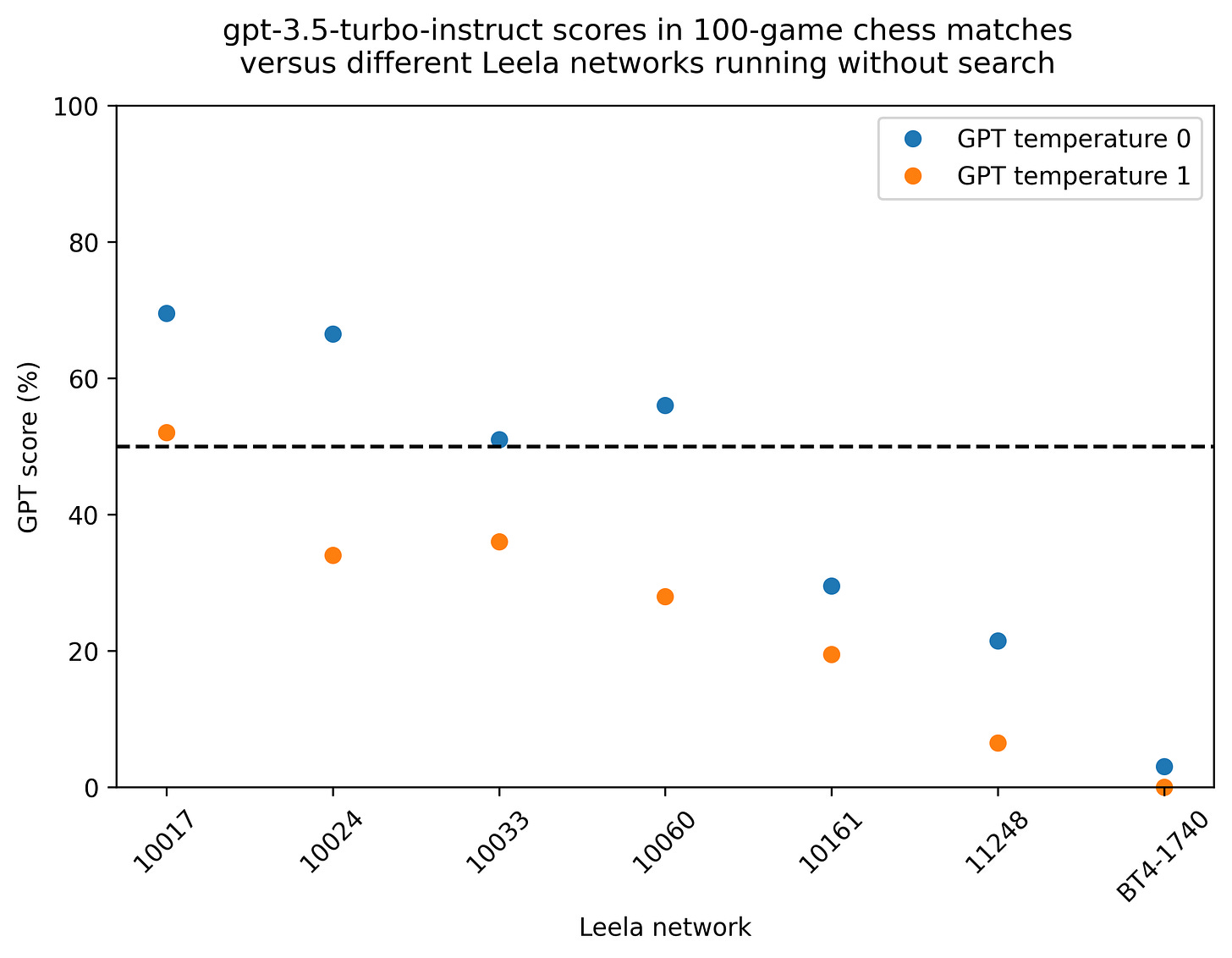
The current best Leela network is BT4-spsa-1740. Against GPT with the default temperature of 1, BT4 was victorious 100-0.
But at a temperature of zero, GPT won a game! Four other games were drawn, making the loss 97-3, which is honestly closer than I had expected. GPT’s win came from playing the Dragon against White’s Yugoslav Attack; Leela allowed the thematic …♖×c3 exchange sacrifice and soon gave up a full piece.
The draws were:
A symmetrical English (GPT Black) which saw pieces vacuumed off into a 0.00 bishop endgame, repetition.
A Sicilian Nimzowitsch (1.e4 c5 2.♘f3 ♘f6) in which Leela (Black) blundered a tactic giving GPT a full rook; GPT soon repeated moves.
An old-school 6.♗g5 Najdorf in which Leela (White) sacrificed two pieces in a kingside attack, won one of them back, then forced a perpetual in a position that Stockfish evaluates as +1.
A 4.♕c2 Nimzo totally dominated by Leela (White), which repeated moves when up a rook.33
So how about older Leela networks? I tried six from the 2018’s test10 run. In all cases GPT scored much better with a temperature of zero rather than a temperature of 1, and I’ll leave the temperature=1 results to the graph and table below.
Network 11248, which took Leela to its first TCEC Premier Division, won 78.5-21.5. Network 10161, which won the TCEC 4th division, won 70.5-29.5. The most-trained network which GPT beat was 10060 from early July 2018, 56.0-44.0.
The trend in the results, with GPT doing worse against more advanced Leela networks, is not quite smooth:
Network Temp. Leela Draw GPT
10017 0 21 19 60
10017 1 40 16 44
10024 0 20 27 53
10024 1 58 16 26
10033 0 35 28 37
10033 1 55 18 27
10060 0 34 20 46
10060 1 65 14 21
10161 0 60 21 19
10161 1 75 11 14
11248 0 66 25 9
11248 1 91 5 4
BT4-1740 0 95 4 1
BT4-1740 1 100 0 0As I watched the results trickle in, I had the feeling that GPT was better on some families of openings than others. But grouped by ECO letter, there wasn’t much of a pattern: 37.1% overall against test10 networks for the ‘A’ openings (flank pawn) was the lowest, and 40.8% for the ‘C’ openings (1.e4 e5 and 1.e4 e6) the highest. The difference is in the direction that I’d expect – centre-pawn openings are more common, so GPT would likely have been trained more heavily on them – but the magnitude of the difference is not large.
Playing against GPT myself
When I lost 8-2 to in a 3min+2sec increment blitz match to gpt-3.5-turbo-instruct, I had left GPT’s temperature setting at 1, because it was the default. After seeing the improved performance against one-node Leela at zero temperature, I tweaked my setup, leaving the temperature at 1 for the first ten moves (to allow for some opening variation) and setting it to zero thereafter (unless there was a text completion that was not a legal move, in which case I tried again with a temperature of 1).
I played ten blitz games against it (no video recording), losing 9-1, the 1 coming from two draws. Games are in this Lichess study. If we naively convert the scores into Elo differences, then at temperature of 1, GPT was about 240 points stronger than me at this time control; at zero temperature it’s about 380 points stronger than me.
I don’t want to lean too hard on those numbers, which are sensitive to small changes (e.g. if I’d converted the bishop-up ending I had, the naive rating gap would be 300 points; and human players can easily swing 100+ points based on fatigue). It didn’t feel obviously stronger than previously – it crushed me both times. But between my own experience and the one-node Leela results, I would guess that the difference between a temperature of zero and a temperature of 1 is about 100 to 200 Elo points.
4. A closing section
This was fun and educational.
Some interesting related work from DeepMind last year was a neural network trained to play chess specifically without search. They put it on Lichess as a bot, and report that it reached a blitz rating of 2895 when playing against humans, about 300 points higher than LazyBot, which is one-node Leela. Rather than using self-play, DeepMind trained their network to predict the moves of Stockfish 16.
Against other bots it only played at 2300; my immediate reaction is to agree with the National Master they talked to, that there’s a class of tactics that regular engines will systematically find and humans often won’t, and the neural network also misses them because it can’t search. But the authors also consider some weird endgame behaviour as a contributor.
Another project that looks very interesting is Yosha Iglesias’s Oracle, which uses both gpt-3.5-turbo-instruct probabilities and Stockfish to predict human moves; I haven’t studied this closely at all, but she reports that Oracle matches a greater percentage of human moves than regular engines do, thanks to the GPT influence.
In its mercy, OpenAI still allows us to pay for gpt-3.5-turbo-instruct completions via its API. The playground page for it is being removed in March, and I worry that the API endpoint will disappear as well. This company not only wants to automate me out of a job, but it might take away my favourite chess-playing language model. Rude!
Officially called Leela Chess Zero; often abbreviated lc0 or lczero; usually referred to as just “Leela” in the chess community.
The quote is edited to remove a misconception that I had about how Leela works. I had previously thought that one-node Leela used only the evaluations, but instead it uses only the policy head, as described later.
All positions with up to seven pieces or pawns have been fully enumerated and evaluated, stored in what are called “endgame tablebases”. The Syzygy bases are the most storage-efficient of these, taking up about 18 terabytes. The simplest way to access them is probably via Lichess’s analysis board, which is free.
Under the hood, an integer number of centipawns.
A big part of me would prefer the Top Chess Engine Championship to use a constant 30 seconds or 1 minute per move, so that the results allow us to judge the quality of the chess analysis of the different engines, rather than some combination of chess analysis and time management. But perhaps some engines perform disproportionately better with a 10-minute analysis compared to a 1-minute analysis, and a flat 1min/move wouldn’t allow this to be demonstrated.
The random number ensures that the bot will not always respond to the same moves in the same way.
Bullet chess is usually played at 1 minute each for the entire game; blitz at between 3 and 5 minutes.
Old Stockfish had tables of bonuses for each piece depending on which square it was on. Naively taking the numbers at face value, a white knight on f6 was deemed about two pawns more valuable than on a1.
But the basic old Stockfish piece values are very un-humanlike, with a knight worth 6 pawns in the middlegame for example, or 4 pawns in the endgame. It is not the case that because Stockfish is better than humans, humans should adapt their intuitions to the Stockfish piece values. A comment on Reddit by one of the devs makes various points:
stockfish eval is actually worse than human eval. It's needed to guide search. It thinks completely differently from how human do it that's why not all human concepts are good for sf eval and vice versa;
…
stockfish has a lot of bonuses for passers, so it's kinda balanced around it. This means that if pawn becomes a passer it becomes worth a ton so probably low material value of pawn is a subproduct of this.
Yasser Seirawan does sometimes talk about space in terms of counting squares. Unlike old Stockfish, he counts only squares attacked in your opponent’s half of the board. This will have some correlation with the Stockfish counts, since controlling squares in your opponent’s second to fourth ranks will reduce your opponent’s Stockfish-defined space count.
I had intended to show a short example of how the analysis varies with depth involving one of those tactics where you briefly sacrifice a queen and for a piece and then win the queen back via a knight fork. I gave such a position to Stockfish 11, and despite the line taking five half-moves to resolve, the engine found the sacrifice at every depth from 1 onwards.
It doesn’t always do this though. I haven’t studied the quiescence search much at all, and it remains quite mysterious to me.
This is based on launching Stockfish from command line, setting the position to the appropriate FEN, and running go depth 18. I extracted only a little bit of the output, which unformatted looks like this:
Building Stockfish was straightforward. I used to run Linux, but I decided to stick with Windows when I recently bought a new laptop. I had no problems creating a Visual Studio project from the existing code base. My only brief hurdle was a linker error that was quickly resolved by o1 and would have been just-as-quickly resolved by a Google search to StackOverflow.
The Stockfish search is recursive, and I added an indentation argument to the search function that I incremented for each recursive call, prefixing any output with an appropriate number of tabs. VS Code very nicely supports expanding and collapsing nested blocks, even in .txt files with no language support, making navigation through the log files much easier than it would otherwise have been. I used the TODO Highlight extension to colour a few keywords of interest.
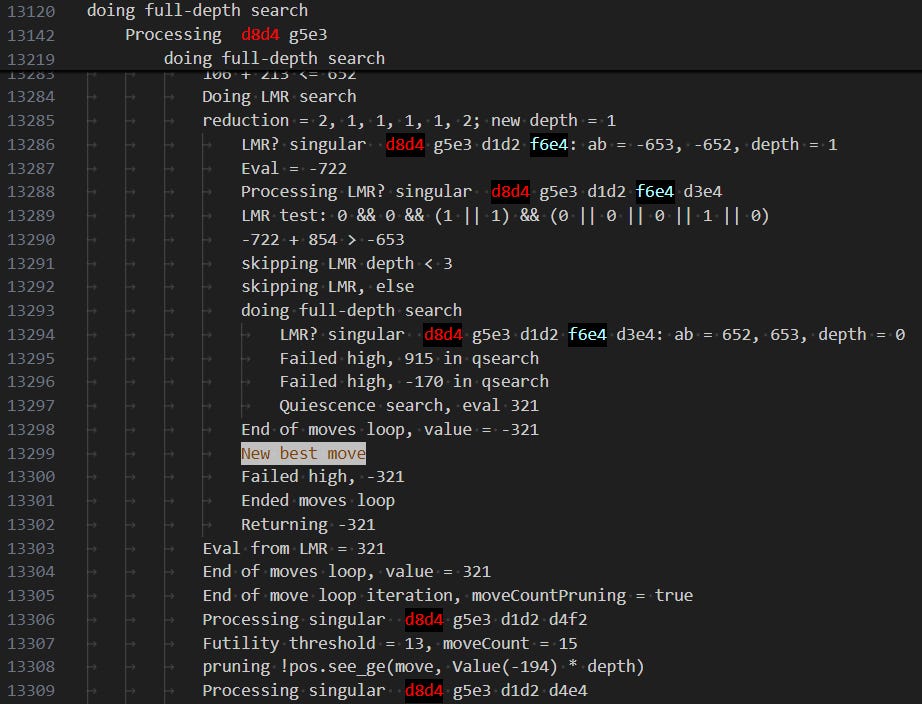
It actually starts the depth=4 search ten times: the aspiration window is wrongly set to the overly extreme [-6.73, -6.48] based on the bad depth=3 eval. It finds an eval above the upper bound (i.e. better for White; Stockfish actually swaps the sign of its evals based on who has the move) in the main line, it gets razored, and eventually it goes back to the calling function, which tries again with a new window, [-6.61, -6.01]. I guess it trusts the previous eval more than that of the one apparent refutation it finds, and it adjusts the window only gradually, and it goes through ten iterations before the eval is within the window.
Hey do you want to see some of my notes for this subsubsection? Here is the evolution of the …♘xe4 analysis. When the search number increases by more than one, it means that the first eval was found outside the current aspiration window and the search for that depth restarted, possibly with a globally adjusted (reduced) depth. I skipped ahead to the successful search and took notes on that file.
The factor of 2.13 in the evals comes from the endgame value of a pawn, used by Stockfish 11 to scale its final output eval; I logged intermediate evals, prior to this scaling. “qsearch” is quiescence search; “TT” is transposition table.
search number (depth; adjusted depth): notes, eval*2.13
1 (1): qsearch +12.38
2 (2): futility pruning, child node, +12.38
3 (3): LMR d=1, futility pruning child node, +12.38
13 (4; 3): futility pruning, child node, +12.38
18 (5; 1): qsearch +12.38
26 (6; 4): LMR d=1, futility pruning child node, +12.38
29 (7): LMR d=3, futility pruning child node, +12.38
32 (8; 6): LMR d=1, futility pruning child node, +12.38
36 (9; 6): LMR d=2, futility pruning child node, +12.38
42 (10): LMR d=6; raisedBeta LMR dxe4 TT cutoff -3.35; prob cut
47 (11; 9): LMR d=5, futility pruning child node, +12.38
52 (12; 8): LMR d=5, futility pruning child node, +12.38
59 (13; 12): LMR d=8, TT cutoff, -5.63
62 (14; 13): LMR d=8, TT cutoff, -5.63
65 (15; 13): LMR d=8, TT cutoff, -5.63
67 (16; 15): LMR d=9, long analysis, -6.26
74 (17; 13): Nxe4 now first move analysed, -7.71
Stockfish 17, which uses neural-network evaluation, gives …♘xe4 as best at depth=12.
The probabilities may not sum to 1; the human-written code will normalise them. The human-written code is also ensuring that only the legal moves are analysed.
To get these I built Leela from source and added some debug logging to search.cc. Unlike for Stockfish, building Leela was relatively difficult for me; perhaps it would have been easier under Linux, I don’t know.
I had to learn a little bit about the meson build system and install a dependency or two, and then I had an error that took me many hours to fix (an apparently missing .rc file), caused by me having no idea what I was doing in Visual Studio. Interested people (zero takes the plural) can read the chat with o1 that finally got me over the line; two earlier questions asked to o1-mini had been fruitless because I was making wrong guesses about what was going wrong.
I write “at most” one new move, because if a move ends the game, e.g. by checkmate, then the search cannot continue down that line any further. Also, as far as I can tell, transpositions are considered distinct, so later on in my iterations there are
1.c4 e5 2.g3
and
1.g3 e5 2.c4,
with the latter line not being extended like I’d have expected.
This division by N_a + 1 and the square root to ensure broadening of the search does not look elegant to my eye. I don’t know if there’s some justification for this particular functional form instead of something else that makes the score lower as N_a increases.
The easiest way to get these probabilities is to run lc0 from command line with the --verbose-move-stats option. At the end of a search, it’ll print various stats and the policy priors for each move.
I didn’t know about that option though, and the way I actually got the probabilities was to do some debug logging from my custom build.
In the following footnote, I list some probabilities for some earlier networks, which use an old file format which is not supported by today’s lc0 executable. I had a lot of trouble with these, and I would have saved a lot of time by using --verbose-move-stats on an old release.
The downloaded old network files are gzipped, and unzip to text files rather than the protobuf format used for the later networks. Trying to follow the instructions to convert to the .pb.gz format (running the net.py script from lczero-training) gave some immediate errors because the number of vectors of weights didn’t match the format expected. After studying the Leela 0.19 source code (this was the last version that runs the old-style networks), I hacked away at net.py to get the counts of the different components correct. I eventually succeeded in outputting a .pb.gz file, but the Leela executable did not load it, and I gave up on this front.
My alternative approach was however eventually successful: building Leela 0.19 from source. Part of this started well, since I’d already built the more recent Leela and now had some familiarity with the meson setup. But the meson build for 0.19 downloaded protobuf 3.5.1, which contains a hash.h file that sets up hash functions for different compilers. For Visual Studio versions >= 2010, it uses std::hash_compare, which has been removed in VS 2022. Microsoft require payment to download older versions of Visual Studio. I tried to modify the meson setup so that it would used a more recent protobuf, but it kept using 3.5.1, perhaps because it was already on my computer by then, and I didn’t try to learn how to get rid of it.
I tried asking o1-mini and Googling about the ways to update code that previously used std::hash_compare without really understanding anything. I then studied the hash.h file, and guided by a comment about adding new compiler support, I removed the VS2010 #define lines and #undef’d two relevant macros, to allow it to fall back to using std::map. Then it compiled!
Still, one could argue that a sufficiently advanced network might be able to deduce the correct move from the policy alone without the need for the PUCT search. It might be able to distinguish between positions where exploration is and is not necessary, sending probabilities towards 100% where appropriate.
So I conjectured that if I gave the above queen-recapture position to earlier, weaker Leela networks, then the probabilities assigned to taking the queen would be less than 82.6%. For the matches between GPT and one-node Leela, I had used a series of networks from the test10 training run from 2018, and I reused these to test my conjecture about the policy probabilities. My conjecture was mostly false, and the details are messy enough that I’ve consigned them to a footnote. The very early networks did indeed assign lower probabilities, but a change in the training regime (more simulated games run on each network) led to a drastic increase in the policy prior, seen in network 10124:
10017: 47.5%
10024: 50.5%
10033: 48.6%
10060: 43.8%
10100: 42.3%
10121: 44.3%
10124: 82.9%
10125: 83.8%
10161: 78.3%
11248: 81.6%
The networks from this run were about 45MB in size, much smaller than the 373MB of the current “big transformer” BT4, but once they hit upon a better training parameter, the probabilities assigned to the simple recapture became similar to the best network of 2024.
The Maia project has a series of networks designed to predict moves based on Lichess rating levels. Its 1900 network gives a probability of 95.6% to the queen capture; its 1100 network 59.8%.
t3-512x15x16h-distill-swa-2767500.
However, once each candidate move is on the board, the value head even of the older network much prefers the correct move, and it becomes the most common move in the PUCT search by an overwhelming margin.
Even BT-4’s only at 10.9% for 6…♘×e4.
Something is at least mildly inaccurate or unexplained in the evaluations I subsequently list. I log the evaluations using the variable v in SearchWorker::DoBackupUpdateSingleNode(), found in search.cc. While this v variable agrees with the --verbose-move-stats output at the root node and for one move into the search, at greater depths the values diverge. e.g. during the search after 7.♗×d8 my debug log says -0.78. But when I run lc0 -v and enterposition fen r1bBk2r/ppp2ppp/2p5/2b5/4n3/3P4/PPP2PPP/RN1QKB1R b KQkq - 0 7it shows a value for the node of -0.81. I don’t know where this difference comes from.
go nodes 1
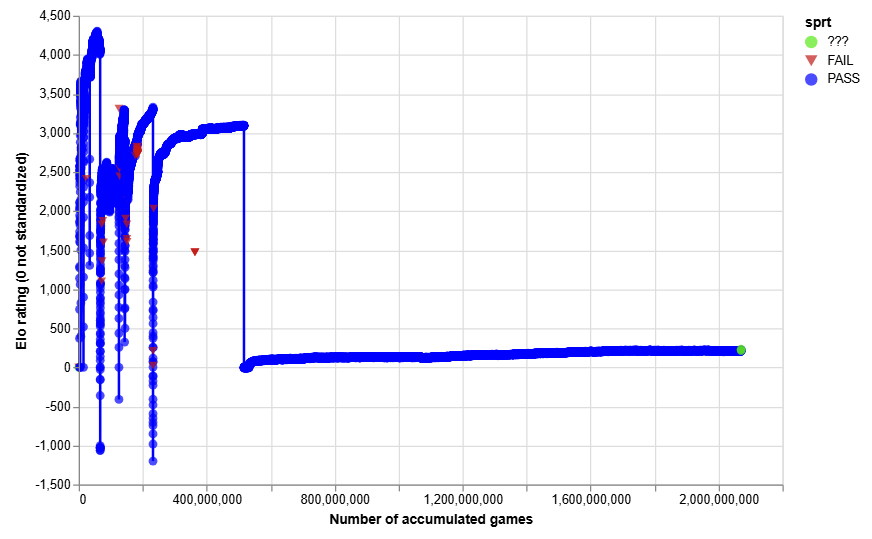
The self-play Elo graph shows a number of sudden dips, corresponding either to resets of the network (especially in the early days) or to recentering of the rating scale:
Many details in this section are based on the LCZero reference page on the TCEC.
Though the big transformers seem to be separate? I don’t know where those ones are; maybe it’s intended that they be downloaded via the lc0 training client.
It probably would have beaten AlphaZero.
Usually a completion that is not a legal move is nevertheless a valid PGN continuation, such as a result string or annotation. Sometimes the notation is garbled, like Bo6. Occasionally it is an illegal move, usually a king moving into check or failing to escape check, but very occasionally a piece teleports across the board or jumps over other pieces.
I wondered if my 2.5-fold repetition rule had cost Leela a half-point here – the final position had not occurred before, so a policy move that didn’t repeat was possible. But I put it into the engine manually and it would have repeated anyway.