Heuristic number theory: prime probabilities

This is not rigorous.

BnF Grec 2483. Deciphering this table is a relaxing puzzle for the interested reader. Using Excel-style labelling, I spot errors in G4, B9, and E9, and there’s a transposition between E8 and F8. In addition to the more obvious redundancies, one iteration was unnecessary. Hints in the final footnotes.

Presumably not original.

What is the probability that a large positive integer N is prime? We can heuristically reason as follows:

• It must not be divisible by 2; half of the positive integers satisfy this requirement, so we get a factor of 1/2.

• It must not be divisible by 3; two thirds of positive integers satisfy this requirement, even after removing the multiples of 2, so we get a factor of 2/3.

• It must not be divisible by 5; four fifths of positive integers satisfy this requirement, even after removing the multiples of 2 and 3, so we get a factor of 4/5.

• And so on through the primes until sqrt(N).¹

Using a lower-case p to denote primes, an upper-case P for the primality probability, and an equals sign for “should be pretty close to”, we can therefore write

\(P(N) = \prod_{p \leq \sqrt{N}} \left( 1 - \frac{1}{p} \right).\)

Sums are easier to work with than products, so we take the log of both sides:

\(\log(P(N)) = \sum_{p \leq \sqrt{N}} \log\left( 1 - \frac{1}{p} \right).\)

Now comes the key step: instead of summing over only the primes, I will sum over all integers n between 2 and sqrt(N), weighting term n by the probability that n is prime. Effectively I’m replacing the “exact” “probability” with an expectation-y probability, and I’ll continue using equals signs because it should still be pretty close.

The point is that we get an equation relating P evaluated at N to P evaluated at smaller numbers, namely

\(\log(P(N)) = \sum_{n=2}^{\sqrt{N}} P(n) \log\left( 1 - \frac{1}{n} \right),\)

and the goal will be to find a function that satisfies such an equation.

The sum should be well-approximated by an integral, so I will change letters to

\(\log(P(x)) = \int_2^{\sqrt{x}} P(u) \log\left(1 - \frac{1}{u}\right) du.\)

Differentiating both sides and applying the fundamental theorem of calculus gives the delay-differential equation

\(\frac{P'(x)}{P(x)} =P\left(\sqrt{x}\right) \log\left(1 - \frac{1}{\sqrt{x}}\right) \frac{1}{2\sqrt{x}},\)

and since x is large, its sqrt(reciprocal) is small, and we can replace the log by its first-order Taylor expansion. This simplifies the equation to

\(P'(x) = -\frac{1}{2x} P\left(\sqrt{x}\right) P(x). \tag{1}\)

Square roots are difficult to work with, so let x = exp(t), and let F(t) = P(exp(t)). Then

\(\begin{align} \frac{dF}{dt} &= \frac{dP(\exp(t))}{dt} \\ &= \frac{dP(x)}{dx} \frac{dx}{dt} \\ &= \frac{dP(x)}{dx} x, \end{align}\)

and so

\(P'(x) = \frac{1}{x} F'(t).\)

Substituting into (1) and cancelling the x’s gives a delay-differential equation for F,

\(F'(t) = -\frac{1}{2} F\left(\frac{t}{2}\right) F(t). \tag{2}\)

The derivative at t is related to the function at t and to the function at t/2. If we had the values of the function at a large t and t/2, then we could imagine numerically solving the equation back towards t = 0, but perhaps no further: halving a positive number will never make it negative.

Let us therefore trial a Laurent series expansion for F(t) with a possible pole at t = 0:²

\(F(t) = \sum_{n=-\infty}^{\infty} a_n t^n.\)

But let us hope that the function does not behave too wildly as we approach the possible pole, and that the Laurent series starts at some finite power k, which will be negative if there is indeed a pole. The left-hand side of (2) will have a lowest power of t equal to k − 1. The right-hand side will have a lowest power equal to 2k. These powers must be equal, so k − 1 = 2k and therefore k = −1:

\(F(t) = \sum_{n=-1}^{\infty} a_n t^n.\)

Inserting this series into (2) gives

\(\sum_{n=-1}^{\infty} n a_n t^{n-1} = -\frac{1}{2} \sum_{n,m=-1}^{\infty} \frac{1}{2^n} a_n a_m t^{n+m}. \tag{3}\)

We proceed by equating like powers of t. The lowest power we can work with is −2, occurring for n = −1 on the left-hand side and n, m = −1 on the right-hand side. This gives

\(-a_{-1} = -\frac{1}{2}\frac{1}{2^{-1}} a_{-1}^2,\)

and therefore

\(a_{-1} = 1,\)

since this coefficient must be nonzero for −1 to be the lowest power of t in the expansion.

The next like power of t to equate is −1, occurring for n = 0 on the LHS of (3) and for (n, m) = (−1, 0) and (0, −1) on the RHS. Since we now know that a_{−1} = 1, we have

\(\begin{align} 0 &= -\frac{1}{2} \left( \frac{1}{2^{-1}} a_0 + \frac{1}{2^0} a_0 \right) \\ &= -\frac{3}{2} a_0, \end{align}\)

and hence a_0 = 0. This is good news, because it sets up a recurrence relation in which all subsequent terms in the series also vanish.

The coefficient of t^r on the RHS of (3) is

\(-\frac{1}{2}\sum_{n=-1}^{r+1} \frac{1}{2^n} a_n a_{r-n}.\)

We can separate out the terms in the sum involving a_{−1} and reduce the sum to being from 0 to r, so that the coefficient of t^r is

\(-\frac{1}{2} \left( a_{r+1} \left( \frac{1}{2^{-1}} + \frac{1}{2^{r+1}} \right) + \sum_{n=0}^r \frac{1}{2^n} a_n a_{r-n}\right). \tag{4}\)

For r = 0, which is the next power we have to equate, the LHS of (3) gives a zero coefficient, and the sum in (4) consists of a single term involving the square of a_0, which is zero. Therefore a_1 = 0, and this process will repeat. The LHS of (3) will give a zero coefficient, the sum in (4) will involve terms a_0 to a_r, which are all zero, thereby showing that a_{r+1} = 0.

The Laurent series for F(t) therefore consists of a single term,

\(F(t) = t^{-1},\)

and therefore

\(P(\exp(t)) = \frac{1}{t},\)

or

\(P(x) = \frac{1}{\log(x)}.\)

The probability that a large positive integer N is prime should therefore be pretty close to 1/log(N), 🎉🎉🎉which is the right answer 🎉🎉🎉.

Behind the scenes: error-riddled chats with o3-mini-high.³⁴

1. The “even after removing multiples of…” bit was not obvious to me, and I asked o3-mini-high for help. Let p_n be the nth prime. We would like to remove multiples of p_1, p_2, …, p_{n−1}, and see what fraction of the numbers remaining are not divisible by p_n.

Let us work modulo M = p_1 * p_2 * … * p_n. The Chinese remainder theorem, applied to this case, says that given an integer x and integers a_1, …, a_n, the system of congruences

\(\begin{align} x &\equiv a_1 \pmod {p_1} , \\ x &\equiv a_2 \pmod {p_2}, \\ & \hspace{0.53em} \vdots \\ x &\equiv a_n \pmod {p_n} \end{align}\)

has a unique solution modulo M. Now:

• there are M combinations of remainders a_i modulo the various p_i.

• there are M remainders modulo M.

There is therefore a one-to-one correspondence between the integers mod M and the combinations of remainders mod p_i. So for any combination of a_1, …, a_{n−1} values, there will be p_n numbers left over, and precisely one of those will be divisible by p_n. The numbers not divisible by primes p_1 to p_{n−1} is the set of all numbers left over from combinations in which all of a_1 to a_{n−1} are nonzero. Each one of these combinations leaves a fraction 1 / p_n divisible by p_n, and there are no intersections, so the fraction of numbers left over that are not divisible by p_n is (1 − 1/p_n).

2. Might there be a shortcut here? I’m not sure if going for the full infinite series is needed.

3. Hint for introductory puzzle 1: Gamma is the third letter of the Greek alphabet.

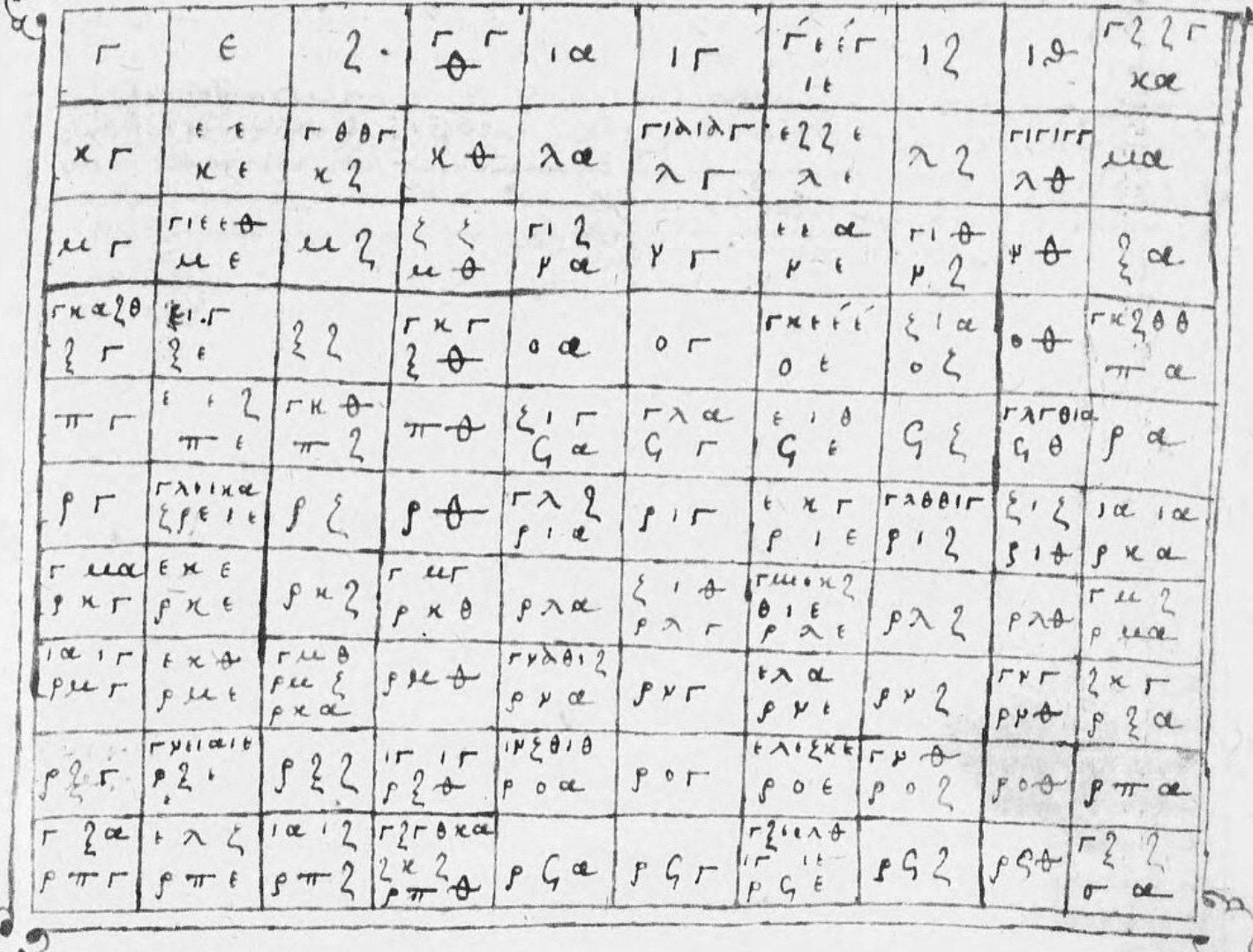
4. Hint for introductory puzzle 2: It’s one of these, but it remains a satisfying exercise to understand it even knowing this context. I was actively looking for a picture like this to introduce the post, and even after a surprisingly helpful Deep Research found a couple for me (I had been flailing around on Google, lost in Greek and Arabic), it took me some time to recognise what was going on.

The 14th-century manuscript is of Nicomachus’s 1st/2nd-century Introduction to Arithmetic (with commentary from the 6th century), and I was originally going to write an extended footnote discussing other manuscripts of this document and the presence or otherwise of the table in the puzzle, which I assume is not present in Nicomachus’s original. For example, the second true positive found by Deep Research, written with different handwriting, contains many of the same errors (though it fills in the gap in B9) – at least one of the scribes was copying numbers without checking them. But, now that I have my bearings in this subject and can approach it semi-systematically, I have enough material to spin it out into an esoteric separate blog post, which should be finished in a week or two.