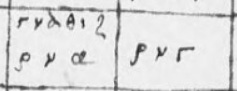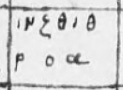The sieve of Eratosthenes is a way to systematically find prime numbers: remove all the even numbers apart from 2, then remove all the multiples of 3 apart from 3, then all the multiples of 5 apart from 5, and so on through the primes. This systematically removes all the composites up to the square of the last prime whose multiples are removed; the remaining numbers are therefore the primes.
A student working with pen and paper would probably cross out the composites from a grid of numbers; on a computer the process may be shown in colourful animated gif form:
The essence of this algorithm is very old; Eratosthenes lived in the third century BC. None of his writing survives though, and the attribution of the sieve to him comes instead from Nicomachus’s Introduction to Arithmetic, written somewhere either side of 100 AD.
For my previous post, about prime numbers, I thought it would be fun to use an old Greek sieve as a preview picture. It was surprisingly challenging first to find one, then to understand what I was looking at. Some of my earliest Googling took me to a History of Mathematics Project page, containing a couple of blurry pages from a book in both Latin and Greek by Richard Hoche, which turns out to be an edition of the Greek Arithmetic text with Latin notes.
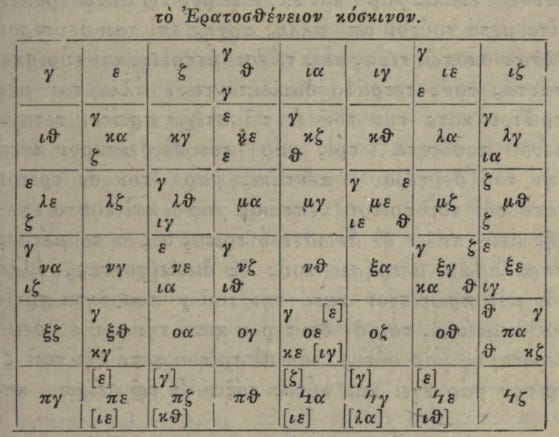
I flicked through it on the Internet Archive, finding a higher-resolution image of the blurry grid that I’d seen on the History of Mathematics page:
I like to think that you instinctively recoil from this picture in total or near-total incomprehension; it looks like heavenly script, as the Chinese say. The grid was thoroughly bewildering to me. I learned enough of the Greek alphabet while studying maths and physics to be able to sound out Eratostheneion in the title, but the rest of it was an intimidating wall of letters and brackets.
I asked ChatGPT-4o what the significance of the Greek letters in the picture was. It said that it was a sieve of Eratosthenes (OK, that’s in the text at the top that I deliberately included to help it), that they were Greek numerals (seems reasonable), and that the numbers in brackets were the primes left over after the sieve (clearly wrong, since the primes aren’t all near the end).
Perhaps because ChatGPT’s conclusion was so wrong, I didn’t follow the correct lead that it gave me, that of the Greek numerals. Instead I looked at it with eyes that glazed over very quickly. In this self-indulgent post, I describe my meandering journey first to understanding this presentation of the sieve, and then down a pleasant rabbit-hole of old Arithmetic manuscripts, eventually finding my way to an existing scholarly literature on the subject.
I could surely have reached my destination more directly. Instead at each step I thought I might be near where I would finish, but chasing down details would reveal a wider landscape with more paths to investigate.
The key breakthroughs in my search were:
A surprisingly useful Deep Research – the first time I’d tried it – which succeeded in finding a couple of manuscripts containing the sieve.
Finding Martin Luther D’Ooge’s English translation of Arithmetic, published posthumously in 1926, which contains a list of the Greek manuscripts that he’d inspected or was aware of, and some discussion of the complicated relations between them.
Realising that if I clicked on the appropriate link in Biblissima, I could get a list of all of the Arithmetic manuscripts in the collections in its database.
Googling, by chance, to Fabio Acerbi’s 2020 paper, ‘The Textual Tradition of Nicomachus’ Introductio Arithmetica and of the Commentaries thereon: A Thematic Cross-Section’.
Early failures
I had two other initial leads in my quest for an old handwritten Greek sieve of Eratosthenes. The Wikipedia article on Nicomachus contains a page from an Arabic Arithmetic manuscript held at the British Library. Googling the technical-looking part of the caption, ‘Oriental Manuscripts, Add MS 7473’, led me to a digitisation at the Qatar Digital Library.
The ‘About’ section tells us that the manuscript was copied in 1242 and contains twenty texts, with what I was looking for towards the end: ‘(15) Nicomachus of Gerasa (نيقوماخس الجراسيني), al-Madkhal ilá ‘ilm al-‘adad (المدخل إلى علم العدد) (ff. 122r-164r)’.
In books, the two sides of a page are counted separately. With manuscripts, the usual practice is to count each folio once only, distinguishing the two sides by the terms ‘recto’ and ‘verso’. Arabic is written from right to left; when a manuscript is opened to show two neighbouring “pages”, the one on the right might be folio 14 verso, or ‘f14v’, while the one on the left is the recto side of the next folio, f15r.
(A corresponding example for a manuscript in a language written left to right would have f14v on the left and f15r on the right.)
I went to f122r and clicked left through the folios. There were some tables with numbers in them, some with Eastern Arabic numerals and some with Abjad, but nothing that looked like a sieve of Eratosthenes. That History of Mathematics page has some excerpts, but the grid of Abjad numerals there is just a times table. I know the Arabic alphabet well enough to sound out consonants and long vowels, but I can’t read the language. I moved on.
I searched Google for ‘nicomachus introduction to arithmetic manuscript’, which turned up a digitised version from Cambridge University. I flicked through the folios; no sieve.
ChatGPT-4o purported to transcribe and translate the Greek handwriting, but I was unconvinced by the transcriptions. (Later I used it for some printed German text, and its transcriptions were good.)
Deep Research
By now I had spent half an hour or more clicking through centuries-old writing in two languages that I couldn’t understand (my Greek is no better than my Arabic), failing to find a good preview picture for a blog post that would be read by perhaps twenty people. I thought it would be worth trying Deep Research, of which I’d read wildly varying reviews. I was not optimistic – surely looking through scanned pictures wouldn’t be its strength. But I pay for ChatGPT and get ten of these a month, so I tried it:
I would like old representations of the sieve of Eratosthenes represented as a table, as it would be today. The earliest description of the sieve was by Nichomachus [sic], and perhaps a manuscript of his 'Introduction to Arithmetic' dating to the Middle Ages contains such a table.
It asked for some clarifications. “Are you looking for scanned images or digital reproductions of medieval manuscripts that depict the Sieve of Eratosthenes in table form?” Yes. “Would you like the modern table representation side-by-side with the historical versions?” No. “Are you interested in representations strictly from Nichomachus' [sic] 'Introduction to Arithmetic', or also other medieval manuscripts that may depict the sieve?” Other medieval manuscripts are also fine.
Sixteen minutes later it had completed its search, finding a manuscript in Kharkiv made available online (for now?) by the Library of Congress,1 and another in Paris, digitised by the Bibliothèque nationale de France. The latter was likely older, dated to the mid-14th century.
The Deep Research gave me some more suggestions, scanned copies of Boethius’ McBoatFace De Institutione Arithmetica, which were older still. I enjoyed idly clicking through his tables of Roman numerals, but there was no sieve of Eratosthenes. Deep Research was working off text descriptions of the manuscripts rather than looking through the images itself, making overly optimistic guesses about the content, and producing confidently-declared false positives.
But the Nicomachus manuscripts it found were true positives! I started with the Paris manuscript, Grec 2483 (older would be better for a preview picture), and clicked through the folios, which have both-sides numbering like modern pages. Nicomachus’s text was in the middle, surrounded by later commentary from John Philiponus (6th century).
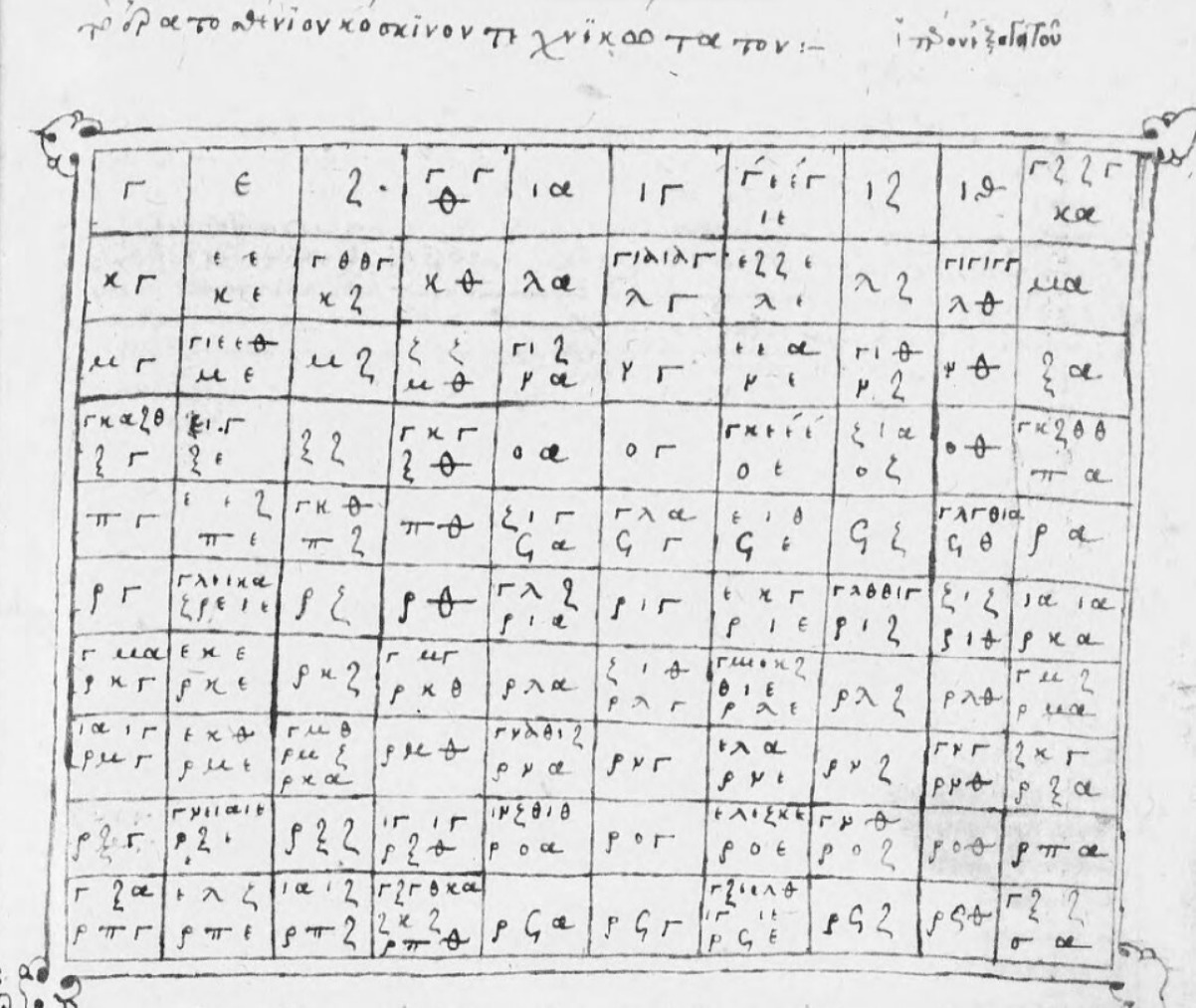
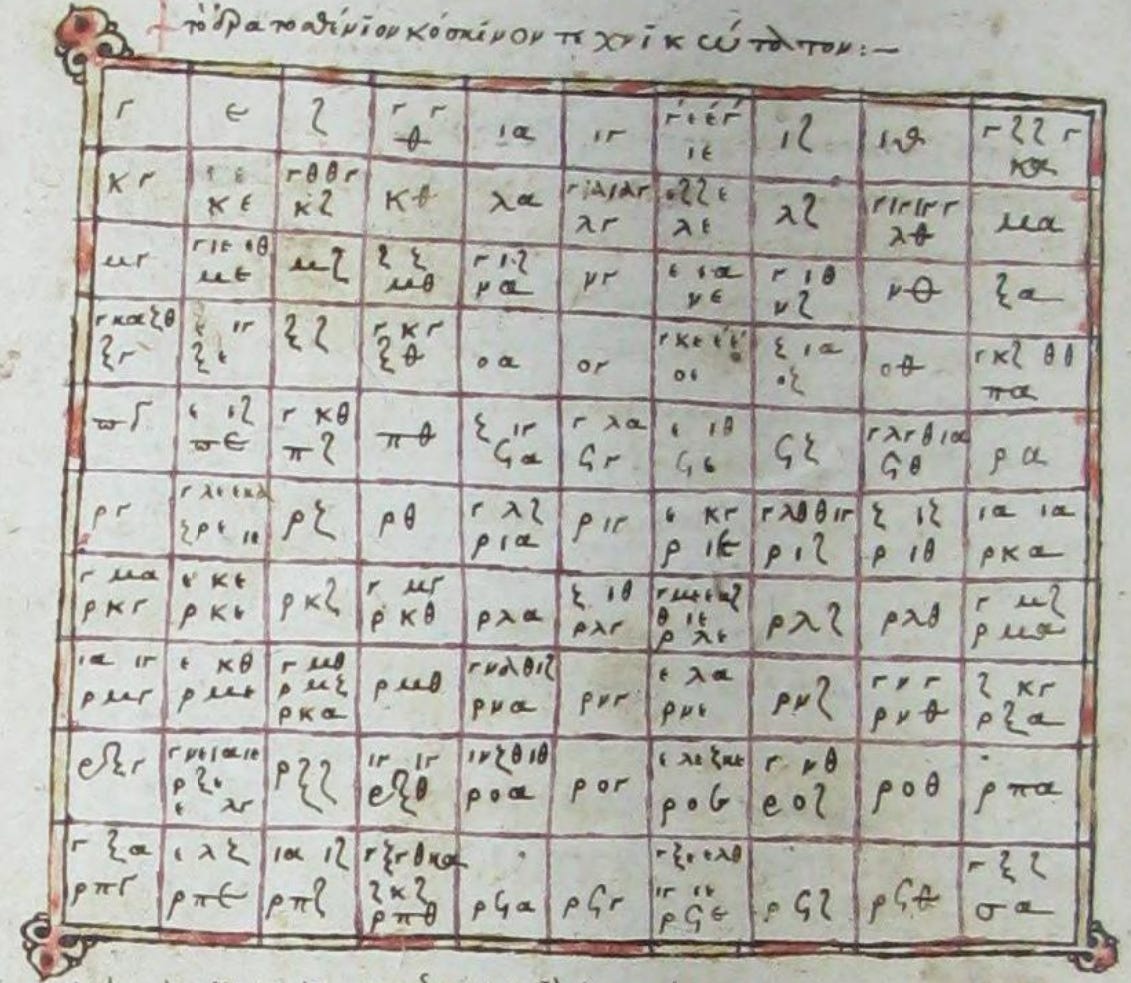
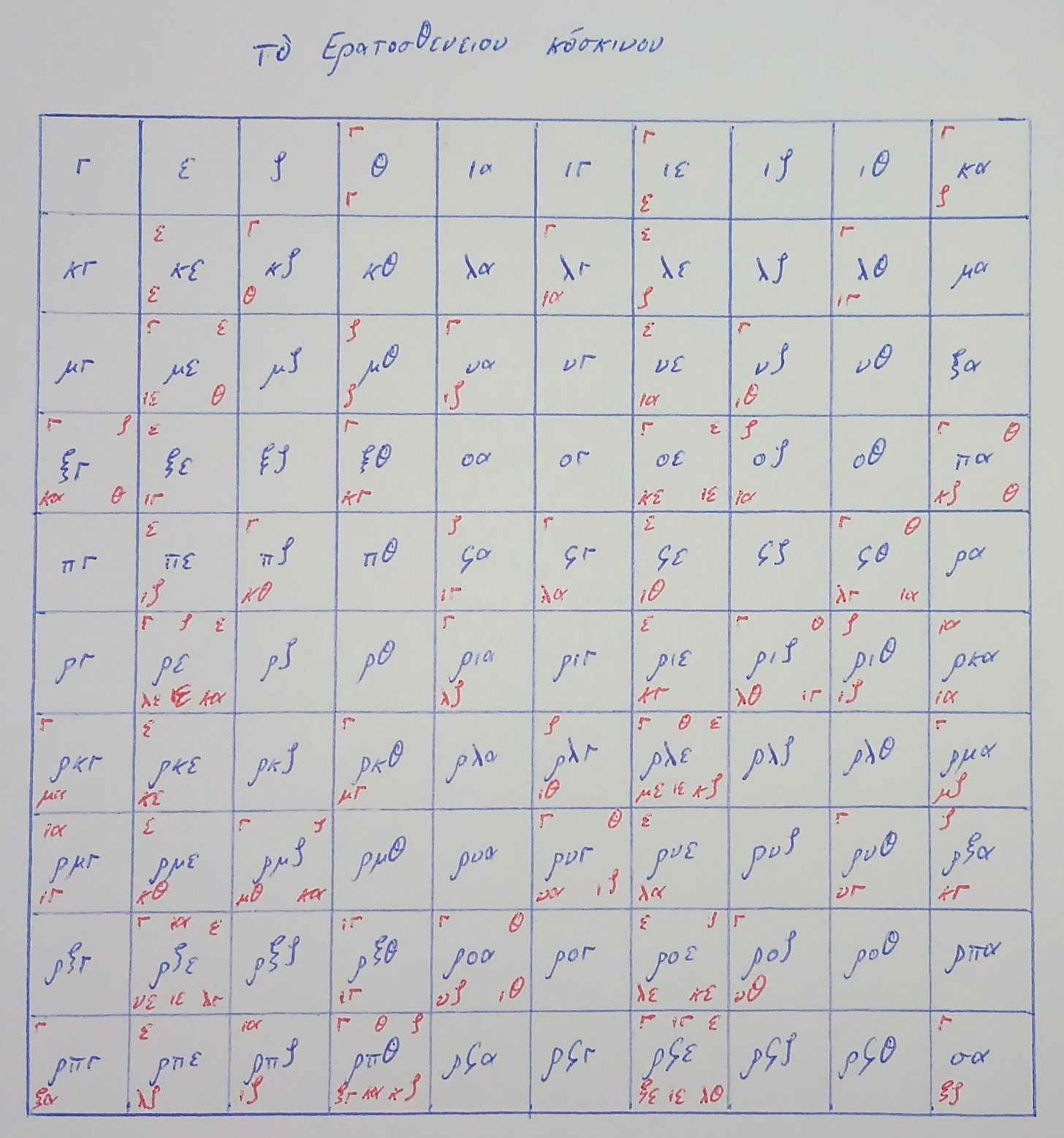
Onward I clicked, and then there it was, page 75:
I cross-checked with the printed Greek sieve from Hoche’s book. The first cell was a gamma, handwritten in upper-case while printed in lower-case. Then an epsilon. Then a zeta (and a dot?). Then two gammas and a theta, differently arranged in the handwritten version, but the same characters nevertheless. I was clearly looking at the right page. I would not have discerned the handwritten Ερατοσθενιον if it hadn’t been followed by the clearer-to-me κοσκινον.
I think by now that I had briefly looked at the Wikipedia article on Greek numerals, but I retained nothing from it, instead staring at these Greek characters as though afresh. The fourth cell looks like a face with gammas for the eyes and a theta for the nose. I can’t remember how long I stared. Gamma is the third letter of the Greek alphabet. Epsilon is the fifth. Is that it? Zeta is the sixth, but never mind, that’s it! These are odd numbers: 3, 5, 7, then 9, and 9 is 3 squared and there are two gammas (3) in the 9 square. Then two more primes 11 and 13, then 15 is 3 times 5. And, this scribe emphasises, 15 is also 5 times 3.
The Greeks must have considered the even numbers obviously superfluous to a search for primes greater than 2, leading to a representation of the sieve that looks, in shape, very different from what I’m used to.
Greek numerals are a base-10 representation, but the characters vary by position. As I absorbed by osmosis, α is 1, but only when it’s in the units column. The number 11 is written as ια, with ι being 10. There is no representation of zero: 101 is ρα, with ρ on its own being 100. I have become very familiar with the numerals for the odd units digits, for which I’ve had many times more repetitions than the numerals in higher positions. I couldn’t tell you what 40 is without looking it up or counting along an old Greek sieve of Eratosthenes, but I can rattle off α, γ, ε, ζ, θ.
α γ ε ζ θ 1 3 5 7 9
ια ιγ ιε ιζ ιθ 11 13 15 17 19
κα κγ κε κζ κθ 21 23 25 27 29
λα λγ λε λζ λθ 31 33 35 37 39
μα μγ με μζ μθ 41 43 45 47 49
να νγ νε νζ νθ 51 53 55 57 59
ξα ξγ ξε ξζ ξθ 61 63 65 67 69
οα ογ οε οζ οθ 71 73 75 77 79
πα πγ πε πζ πθ 81 83 85 87 89
ϟα ϟγ ϟε ϟζ ϟθ 91 93 95 97 99
ρα... 101...(Wikipedia tells me that zeta represents 7 because the obsolete letter digamma was used for 6. The numerals were often written with an overbar.)
I picked up a pen and patiently produced a sieve in this form using Western Arabic numerals, optimistically starting after some unrelated scribbling and spilling over onto a second page.
During this calming exercise, I found some errors in the manuscript. I wasn’t confident of the first one I saw: 75 is 3 × 25 and 5 × 15, but the manuscript’s copyist omitted the ι in ιε.
Perhaps it was just a bad scan? (I’m now pretty confident that it’s a genuine error.)
The next error is unambiguous even for an amateur who can’t read Greek: the scribe has placed the factors of 153 in the 151 square.
Factors are quite consistently shown in pairs throughout this sieve, so I count the omission of 33 from the 165 cell, for which there is space in the lower-right, as an error:
Finally, since 171 = 3 × 57, the first ι in the 171 cell should be a γ.
Such pedantry does more than give me the satisfaction of knowing that I’m better at arithmetic than a 14th-century scribe, though that is no small thing in itself. The other Arithmetic manuscript found by Deep Research was the one in Kharkiv, which has almost an identical sieve (f78v):
Many of the errors are the same – the 165 cell has its factor of 33 now, but there’s the same swapping of the 151 and 153 factors, the same ι for γ in 171. The absence of a clear ι in what should be ιε in 75 is what now makes me confident that that cell contains a scribal error, rather than a bad scan. At least one of these two copyists was copying a source without checking the numbers!
(Despite the Library of Congress dates for Kharkiv (1300-1499) suggesting that the Paris manuscript probably came first, Acerbi’s table of manuscripts says that the latter is a copy of the former. I note with light amusement that the adornments on the table’s corners weren’t copied exactly, the top-right corner in Kharkiv being plain.)
I now had two lines of questions that I wanted to pursue:
Given that some manuscripts contain the sieve and some don’t, and given my bizarre and incorrect recollection that early Greek copies of Euclid’s Elements were written without diagrams, I strongly suspected that Nicomachus’s original contained only the description of the sieve, and not its representation in table form. When did later scribes start to introduce the tables? What’s the oldest sieve of Eratosthenes that I could find?
Were there other Arithmetic manuscripts that have a sieve with the same errors as seen above? How did these errors propagate as one scribe corrected or imperfectly copied another?
D’Ooge
While Googling around the subject, I stumbled on a review of a then-recently published English translation of Arithmetic by Martin Luther D’Ooge, which is online. D’Ooge died in 1915 having completed the translation itself but not the accompanying material that would be part of an edited publication; the extra commentary and discussion was written by two of the translator’s former colleagues at the University of Michigan, and the book was published in 1926.
The first thing I checked was whether or not a diagram of the sieve is present. It is not, despite being described in words; more evidence that its representation was an addition by later scribes or commentators.
But the table of contents also shows ‘The Manuscripts and Text of the Introduction to Arithmetic’, and this chapter was immensely valuable both for giving me a list of specific manuscripts to look up, and for understanding error propagation through manuscripts.
The simple model is that all extant manuscripts derive from a common ancestor, the ‘archetype’. While copying, a scribe may make a change to the text (deliberately or accidentally), and copies of that manuscript would inherit the change, and possibly introduce new ones.
D’Ooge tells us that Hoche, for his 1867 Greek edition of Arithmetic, worked from nine manuscripts, and considered the Codex Gottingensis the most reliable representation of the archetype’s text. The Gottingensis – the customary use of Latin to refer to manuscripts would present some challenges for me – was dated to the tenth century, much older than the other eight. (More recent scholarship dates it to c. 1300, as I later learned from Acerbi.)
Hoche labelled the Göttingen manuscript G, separating it at times into G1, its original text, and G2, containing text overwritten by a later hand. There were three manuscripts in Munich (‘Codex Monacensis’ followed by different identifying numbers), labelled m, μ, and S. H a manuscript from Hamburg. N from Nuremberg. Γ from Wolfenbüttel (‘Guelferbytanus’). C a ‘Codex Cizensis’, which Google Translate failed to help with, and for which ChatGPT-4.5 hallucinated a dubious Ciza, Croatia.2 P a 1538 book publication in Paris by Wechel, which “deserves to be reckoned among the manuscripts, since the manuscript upon which it was based, apparently an ancient and a good one, has disappeared.”
Hoche grouped the manuscripts into a something akin to a phylogenetic tree, with G1, m, and P stemming from one of the main branches.
But D’Ooge (I will assume that he wrote this chapter, though it might have been written after his death) studied many more manuscripts, and found a good deal of cross-pollination between them, if I may mix biological metaphors. (The more formal term is ‘contamination’.) D’Ooge’s p3 manuscript follows G1, m, and P in having απλως ο τεχνης τιωος where C, μ, and the others listed above3 have απλως πας ο τεχνης τιωος (diacritics omitted, sorry). But at the next variant reading, p3 is in the group with C and μ, having συστειλας το ονομα where G1, m, and P have συστειλας παντων το ονομα. “It must also be observed that manuscripts were frequently compared with one another and variant readings noted down, which doubtless were taken into the text as time went on.”
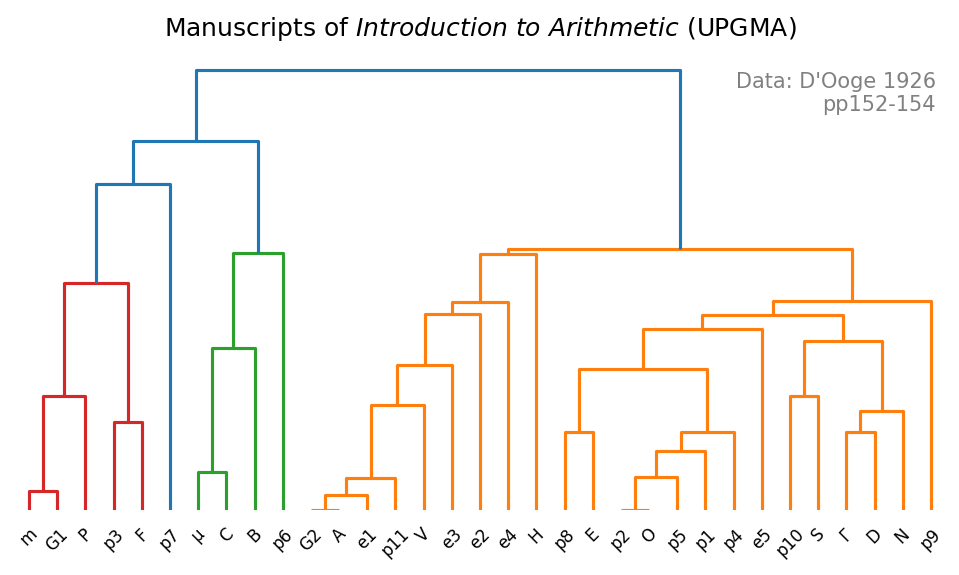
D’Ooge lists 37 variant readings from 34 manuscripts, not all of the manuscripts listed at each point of variance. I thought it’d be interesting to encode this data and vibe-code a dendrogram4 despite the contamination across branches. I have 33 manuscripts included in the data, omitting L because it’s only listed in one reading.
There’s enough agreement with D’Ooge and Hoche for me to be satisfied while looking at this diagram. It is not surprising that some of the main groupings are reproduced: if Hoche could see that G1, m, and P were similar, then they should have small calculated distances between one another and be clustered together in the dendrogram, as happens. C and μ are also found together, though the dendrogram has them more closely related to G1-m-P than to the other manuscripts studied by Hoche.
I would want more systematic data coverage before offering the dendrogram too seriously, though I think it is worth something anyway. My sense is that D’Ooge got a little lazy as the variant readings progressed: early on almost all of the manuscripts are accounted for, but then omissions start to creep in, and there’s a dozen manuscripts missing from the last few points of variance.
I will certainly not be filling in the missing data any time soon: even where the manuscripts are available online, locating specific points in handwritten Greek text would be very difficult for me, and then I would have to correctly figure out what letters I was looking at, also difficult.
Grec 2483, the Paris manuscript that Deep Research had found for me, corresponds to D’Ooge’s p1, sitting unremarkably in the extended orange family of the dendrogram. The Kharkiv manuscript is not listed by D’Ooge.
With much more context now available to me, I returned to Hoche, no longer intimidated by the Latin. I scrolled through the introductory text and started to recognise things.
The same family tree diagram, G the cod[ex] Gottingensis, saeculi decimi, tenth century.
I turned to the page with the sieve of Eratosthenes and typed the surrounding Latin text into Google Translate and ChatGPT-4o, whose translations here are surely good enough for my purposes.
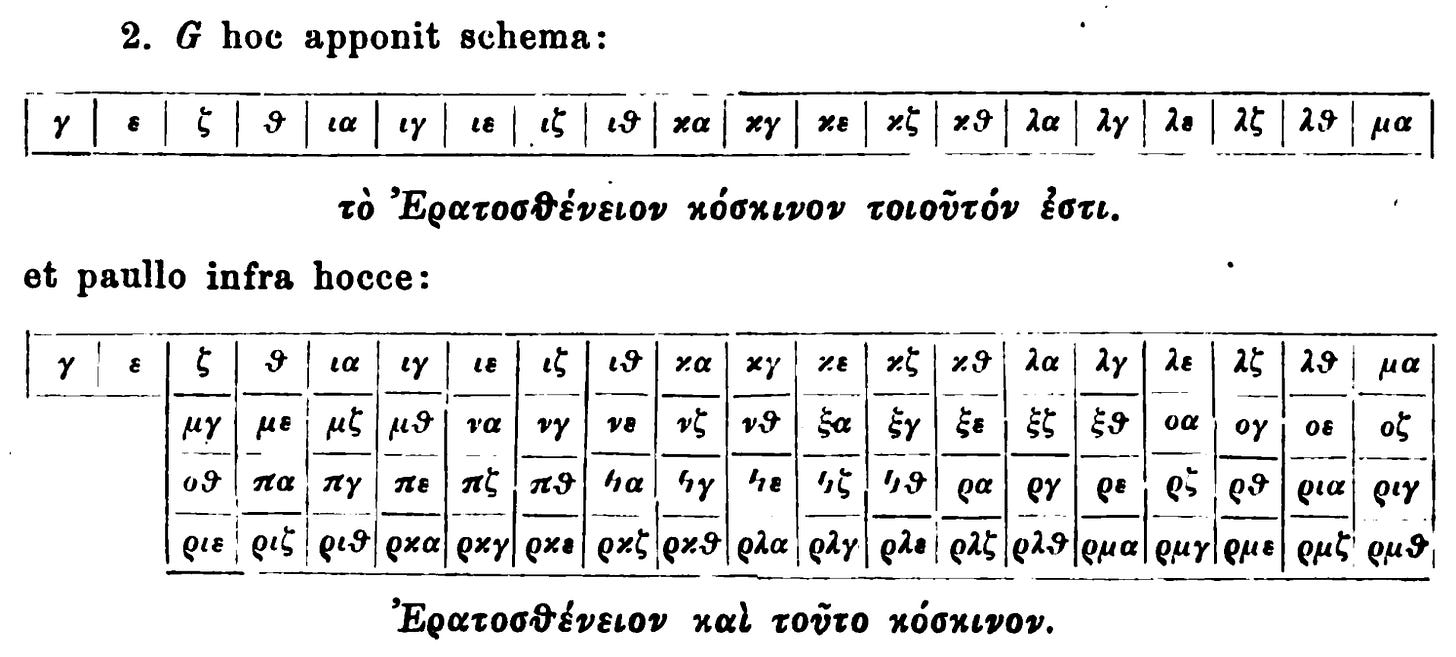
G adds this diagram:
(row of odd numbers in Greek numerals)
and a little further down, this one:
(larger grid of odd numbers)
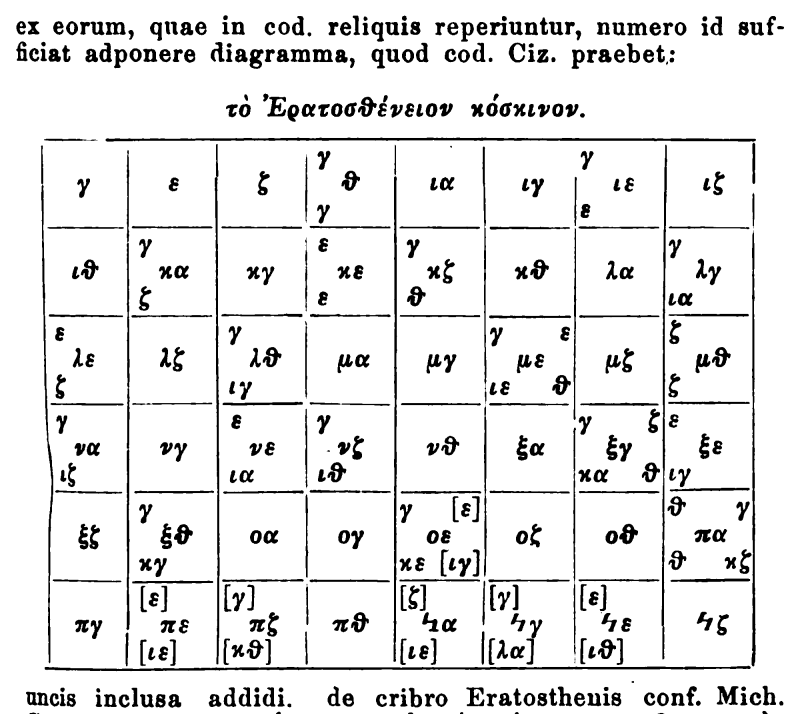
from among those which are found in the remaining manuscripts, it is sufficient to add this diagram, which the Cod[ex] Ciz[ensis] provides:
(sieve of Eratosthenes)
I have added the portion enclosed in brackets.
So the manuscript in Göttingen has a grid of odd numbers unsieved, and the Cizensis has a grid partially completed, a lazy scribe not listing any factors past 81.
The bracketed additions are woeful. Hoche, if I am correctly assigning blame to him, made an off-by-one(-odd-number) error in his multiples of 5, repeating ε (5) and ιγ (13) in the οε (75) square, when ε had already multiplied ιγ to make ξε (65).
This counting error propagates to the next odd multiple of 5, with an erroneous 85 = 5 × 15, but he does get back on track with a correct 95 = 5 × 19 by the end.
There is also a jarringly wrong 91 = 7 × 15 (such a product must end in an ε!), while 77 has been left as apparently prime.
It’s been almost 160 years since the publication of this work, so I assume someone else has already pointed out these errors.
In what was quite a stretch, Nicomachus defined three categories of odd numbers: prime, composite, and composite but relatively prime to another given odd number (i.e., having no common factors with another odd number except for 1). While today we think of the sieve of Eratosthenes as being about finding the primes, a representation which shows all the different factors would also allow for a visual check to see if two odd numbers were relatively prime. Nicomachus does, however, also describe the Euclidean algorithm as a means to test for relative primality.5
He describes the operation of the sieve as working through multiples of all odd numbers, not just the primes, and this is reflected in the sieves seen above, which show, for example, two θ’s (9) in the πα (81) square.
Biblissima
Thanks to D’Ooge’s list of manuscripts, one of which I’d already looked at, I now had many leads. While it wouldn’t contain a filled-in sieve, the most important for the text overall was seemingly G, the Codex Gottingensis. I Googled this phrase and found a Wikipedia article on a 13th-century manuscript of the New Testament. I tried "codex gottingensis" "philol. 66", adding the identifier given by D’Ooge, and found only D’Ooge’s book.
Codex Cizensis also remained a mystery to me; I Googled and failed to notice the snippets of text that said it was in Zeitz, perhaps because Zeitz doesn’t start with a C, I had never heard of that town, and the name didn’t pop out at me. Wechel’s 1538 publication is a book rather than a manuscript, and is on Google Books; no sieve.
The most promising avenue was surely the manuscripts in Paris, of which D’Ooge had listed 12 including one I already knew about. The Bibliothèque nationale de France and its digital library Gallica are a wonderful resource. But sometimes when I Googled the manuscript identifiers – BnF Grec 2481, BnF Grec 2480, … – I would first land on a Biblissima page (for example), part of a French portal for medieval documents. These pages would have thumbnails of the scanned folios, as well as a link to Gallica.
Usually I’d skim through the thumbnails, looking for a possible sieve of Eratosthenes. But one time I thought to click on one of the Biblissima internal links:
And that was the gold mine, a list of 103 manuscripts containing Nicomachus’s Introduction to Arithmetic, many of them having a picture icon indicating that they could be read online.
I looked through the list. Göttingen, Philol. 66, not digitised. No results from a ctrl-F for ‘ci[zensis]’, a continuing mystery. Many identifiers corresponding to D’Ooge’s list, lots of digitisations from the BnF, quite a few from the Vatican.
I started systematically working through the picture-icon links, making notes of folio numbers and screenshotting sieves, which showed a greater variety than the two found via Deep Research. (All my screenshots are in the PDF linked at the end.)
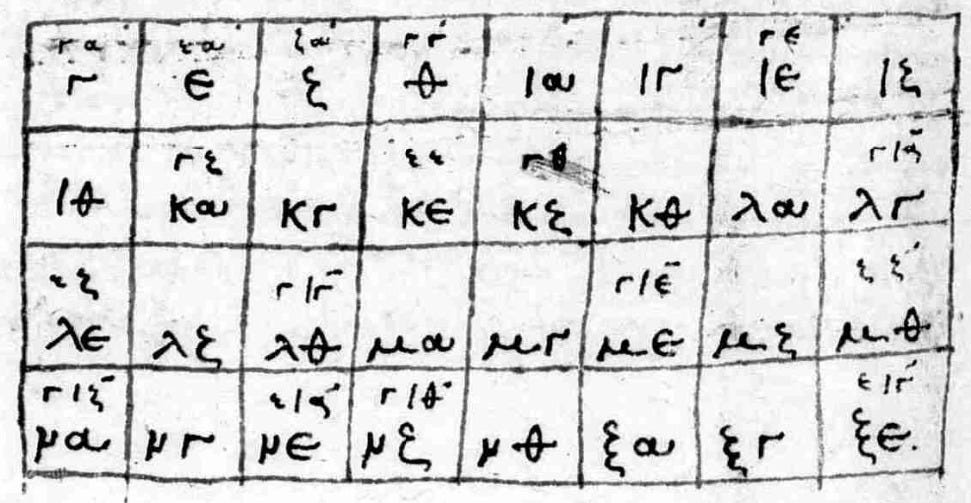

The most beautiful by far, thanks in part to a colourful high-resolution scan, was in Grec 2373. The odd numbers are arranged in a long clockwise array that surrounds the text on three sides, the whole only spoiled by the failure to sieve out multiples of 11 and 13:

The only false positive in the Biblissima list was from the British Library, the link to its Harley MS 6295 having been broken after a cyberattack in 2023; the gradual restoration of the Library’s digital manuscripts is not complete.
The Kharkiv manuscript is not in Biblissima, so the latter must not be comprehensive. I tried going to the individual library websites for non-picture-icon links and found that sometimes the manuscripts were in fact available online (indeed, I had already gone through MS Kk. 5.28 at Cambridge in one of my early failures to find the sieve), though the Gottingensis is not in this category. I slowly added to my collection of screenshotted sieves.
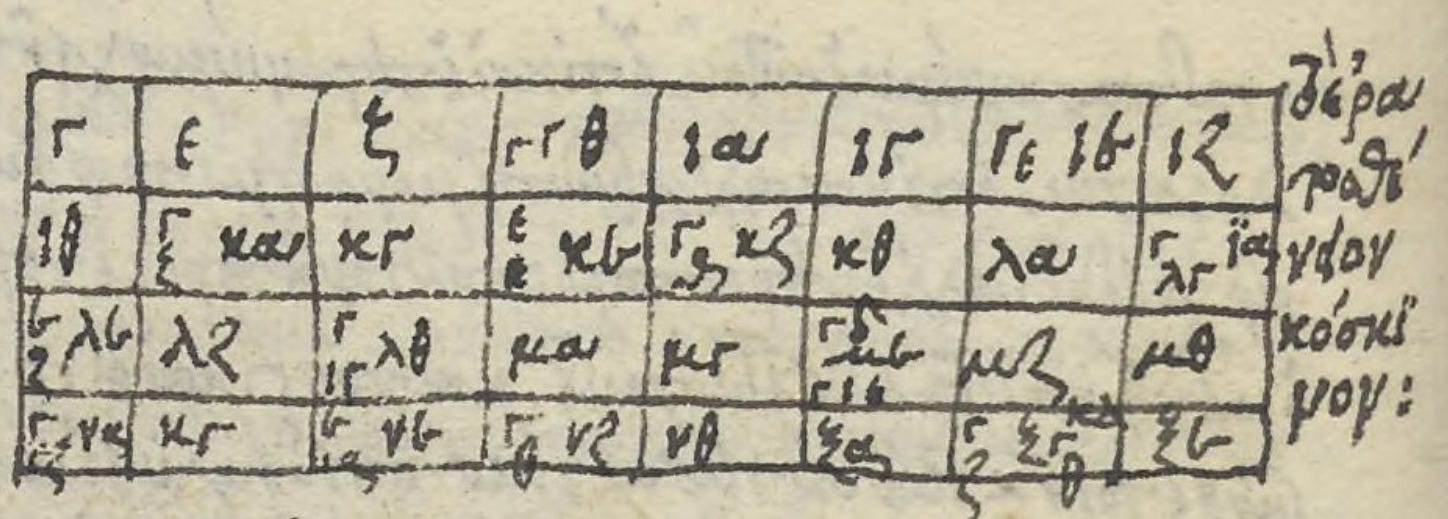
As I grew more accustomed to the Greek numerals, I sometimes spotted an inline sieve in the surrounding commentary, even without the visual aid of a grid to catch my eye.


A Biblissima search for Philiponus’s commentary alone also turns up a few more manuscripts.
Acerbi (2020)
The Codex Cizensis was an annoying loose end. It was presumably not one of the digitised manuscripts listed by Biblissima, but where was it? I Googled and re-Googled furiously, still failing to read the words on the screen in front of me that said that it was in Zeitz. I found a German paper from 1884 which mentioned the codex a few times; I got 4o to transcribe and translate my screenshots from it; no leads.
More promising was a reference Müller (1815), Notitia et recensio codicum mss. qui in bibliotheca episcopatus Numburgo-Cizensis asservantur. 4o translated the title as ‘Notice and review of the manuscript codices preserved in the library of the bishopric of Numburg-Zeitz’. Perhaps Cizensis refers to Zeitz?
A Google search for ‘"zeitz" nicomachus’ got me what I needed: the first result was a 2020 paper by Fabio Acerbi, ‘The Textual Tradition of Nicomachus’ Introductio Arithmetica and of the Commentaries thereon: A Thematic Cross-Section’.
The solution to the Cizensis mystery was suddenly only a minor detail. “Zeitz, Stiftbibliothek 67 (Cizensis 67, Diktyon 72776)”. There was a Zeitz at the end of the Biblissima list; not digitised.
More importantly, Acerbi’s paper showed me that there was an academic literature on the subject that I was playing with when making my dendrogram. The abstract:
The entire textual tradition of Nicomachus’ Introductio arithmetica and of the commentaries and scholia thereon is investigated by using a single, unusually cryptic sentence in Nicomachus’ text as case-study. The relations between the “Recensions” of Ammonius’ lecture notes are also clearly established. Finally, the way an entire exegetical tradition has dealt with such a cryptic sentence is discussed.
Then in the introduction:
I will present a thematic cross-section of the entire manuscript and exegetical record by using a single sentence in Nicomachus’ text as case-study. Of course, this sentence cannot be a chance one. I have selected an unusually cryptic statement if gauged to Nicomachus’ writing standards –so unusually cryptic and unsyntactical as to quite certainly be a gloss that has crept into the text at a deep pre-traditional stage. This happened in fact before the renowned Neoplatonic philosopher Ammonius (early 6th century) held a course on Ar. whose lecture notes make, in the form of a number of “Recensions”, the bulk of the exegetical record on Nicomachus’ treatise. An interesting fact is that a paraphrasis of the test-sentence crept in its turn, as an adjunct (henceforth “Adjunct”) to the very last sentence of Book I, into the text transmitted by a fair majority of the available manuscripts.
My interest in the subject does not extend so far as to read all of this paper, which has many pages of colourful Ancient Greek. It showed me that if I pursued this subject, then there would be an enormous amount of work waiting for me. The scope of this little blog post would not continue expanding until it was a comprehensive analysis of manuscript copying errors, propagation, and correction. I would set my sights lower.
Acerbi writes that Hoche “used a random and quite limited set of manuscripts” for his 1867 Greek edition of Arithmetic, “namely, those readily available to him because they were kept in nearby German libraries. Hoche took the one carried by Gott. philol. 66 as his text of reference, relying on a wrong dating of the manuscript to 10th century.” A footnote says that “It was in fact penned only in the late 13th century, all while using an imitative script”. Disappointing!
Acerbi cites two papers for the revised date of G, De Gregorio and Prato (2003) and Acerbi and Gioffreda (2019). Both of those are in Italian, but you can drop them into NotebookLM and query them in English; it is very fast, and in my judgement (knowing the context, and being able to read French well enough to half-read Italian) it is easily accurate enough for purposes of a blog post. (I would link to mine, but NotebookLM does not allow me to share a notebook publicly.) The first paper matches the handwriting in G to those in other manuscripts, written in Constantinople with a deliberately old-fashioned “archaising” script.
Here is Vat.gr.225, f14r, one of manuscripts claimed by De Gregorio and Plato to have been copied by the same person who copied G:
And here is BnF Grec 2948, f17r, ditto:
G is not online, but the Acerbi-Gioffreda paper from 2019 shows one medium-resolution page of it, of which the following is the clearest sample of writing (f153r):
I won’t argue with the handwriting match. I definitely prefer this pseudo-old-timey writing, in which I can discern a much higher proportion of the letters, to the newfangled 14th-century scrawl. Here is the same passage in BnF Grec 2483, p168:
(See page 79 of Hoche for a printed version.)
It took me the better part of two hours to find this matching passage, despite knowing roughly where in the text it must have been – the full page of G in the 2019 paper shows a diagram containing powers of 3, amongst other numbers, which functioned as a signpost. I’m at the limits of my ability here.
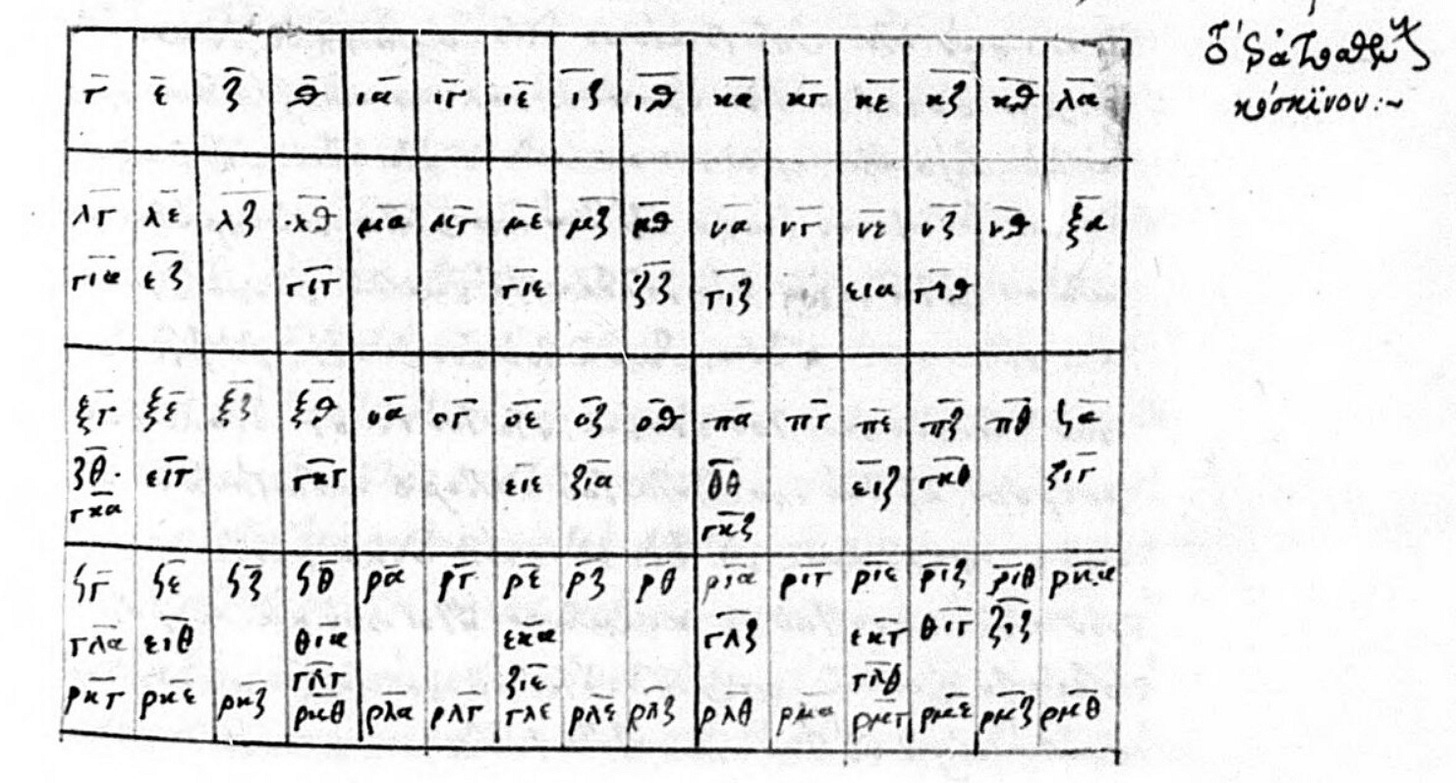
The tables of manuscripts in the appendix to the Acerbi paper provided me with some new ones to search for, and included some comments that were relevant to my observations. The Zeitz manuscript is said to be related to Vat.gr.1411, whose sieve was pleasingly familiar: almost identical to a bracketless version of Hoche’s sieve:
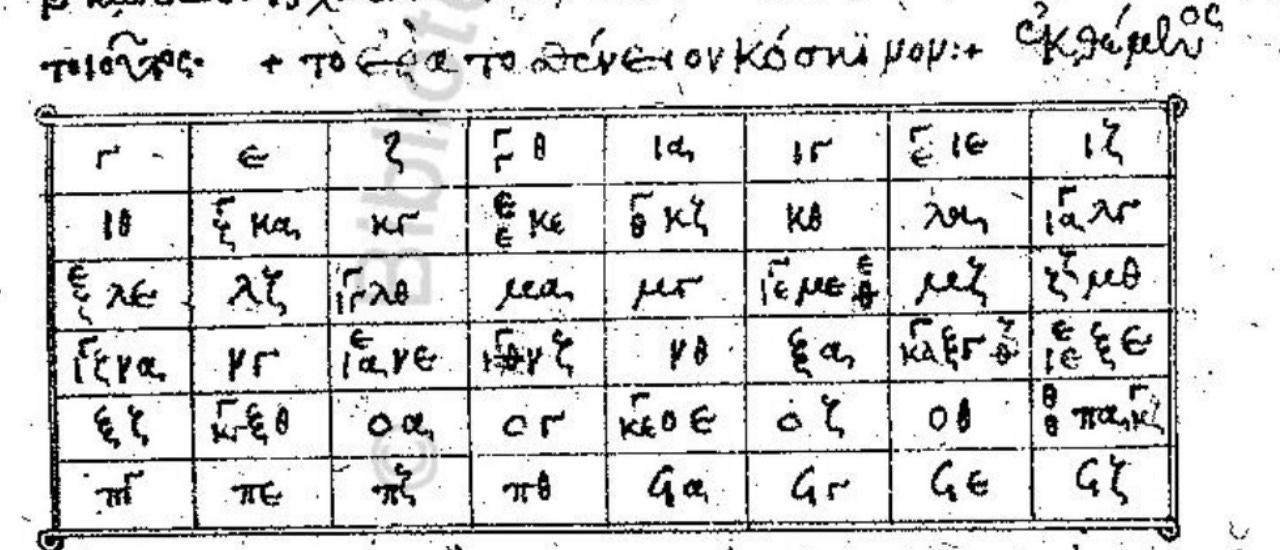
The manuscripts are frequently referred to with abbreviations of place names, many in Latin, which 4o correctly explained for me after saying what great questions I was asking. “Laur.”, the Biblioteca Medicea Laurenziana in Florence. “Marc.”, the Biblioteca Marciana in Venice. “Berol.”, Berlin.
The references all come with Diktyon numbers, which I’d seen in passing in Biblissima but hadn’t looked at. Each Greek manuscript that the Pinakes website/database knows about has an associated Diktyon number, and you can search for it and get information about the manuscript (for example), including dates, owners, academic papers that refer to it, and often a link to a digitisation when available. This was a rapid way to collect links to digitisations without having to navigate library websites.
One of the papers frequently mentioned in Pinakes was another by Acerbi, titled ‘Eliminazioni diagrammatiche’. I was worried that it would be too relevant to this post, and that I’d been scooped.
Diagrammatic Eliminations · The filiations between the manuscripts of the plethoric textual tradition of Nicomachus’ Introductio arithmetica are studied by using conjunctive readings in the diagrams that accompany the text. In this way, about 40 witnesses are eliminated as codices descripti.
Most of the paper is about other diagrams in Arithmetic. NotebookLM told me that its main observation about sieves of Eratosthenes refers to final-square crosses in what I recognised as rows of unsieved odd numbers; the paper shows three such examples.
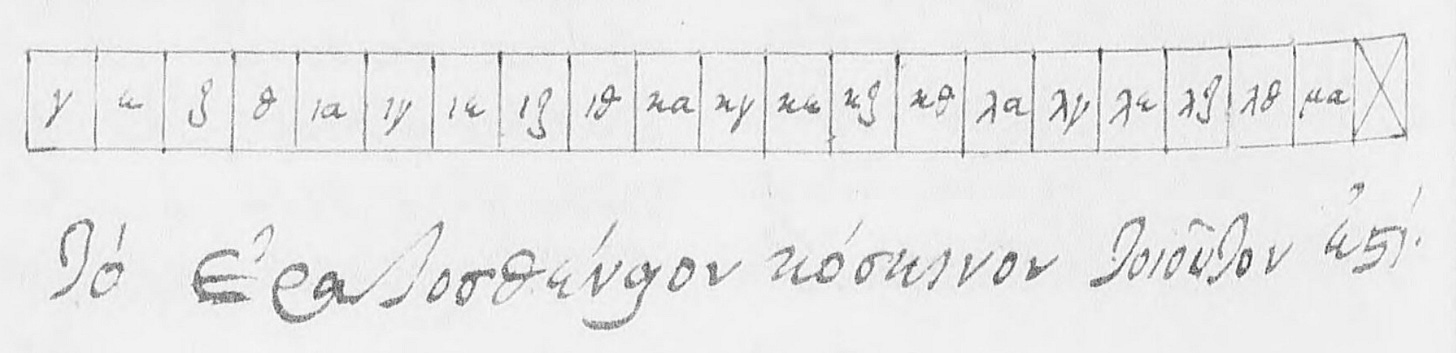
The paper also mentions that Grec 2479 has two sieves of Eratosthenes. I had closed the tab when I found the first one! What an embarrassing blunder! I had one job for this post, and I didn’t know what I was doing. My confidence in writing about this subject took a blow.
I did a second pass over the digitised manuscripts in which I’d found one sieve, and collected another six screenshots.

Clusters
Acerbi’s table of manuscripts tells us that of the two found by Deep Research, Grec 2483 is a copy of the Kharkiv manuscript (for which I now had an identifier, 269-p, 369-c). It was pleasing to have such a tidy explanation for the arithmetic errors they had in common, but it was also in some sense a coincidence.
I found three further sieves with a 10 × 10 grid containing odd numbers from 3 to 201. Grec 2377, f42r (16th century) shows the same errors as in Grec 2483, and its clear writing revealed a couple more that I’d earlier missed: εεα being written instead of ε ια in the factorisation of 55, and εεζ instead of ε ιζ in 85. (I’d earlier assumed that the offending epsilons were smudged iotas, but looking closer I think they’re epsilons.) Grec 2377 also introduces a new error, with a ξι instead of ξε in the factorisation of 195.
Grec 2377 is apparently a “conformal copy” of the manuscript in Berlin (not online), which in turn “stems from Vat. gr. 1411”, whose sieve is the one in the last screenshot above, with a grid ending at 97. And in fact Grec 2377 has two sieves, the other being the grid to 97; somewhere along this line, someone evidently copied from two different sources. Even the locations of the factors within each square are copied: to the sides in the smaller grid, generally to the top in the larger.
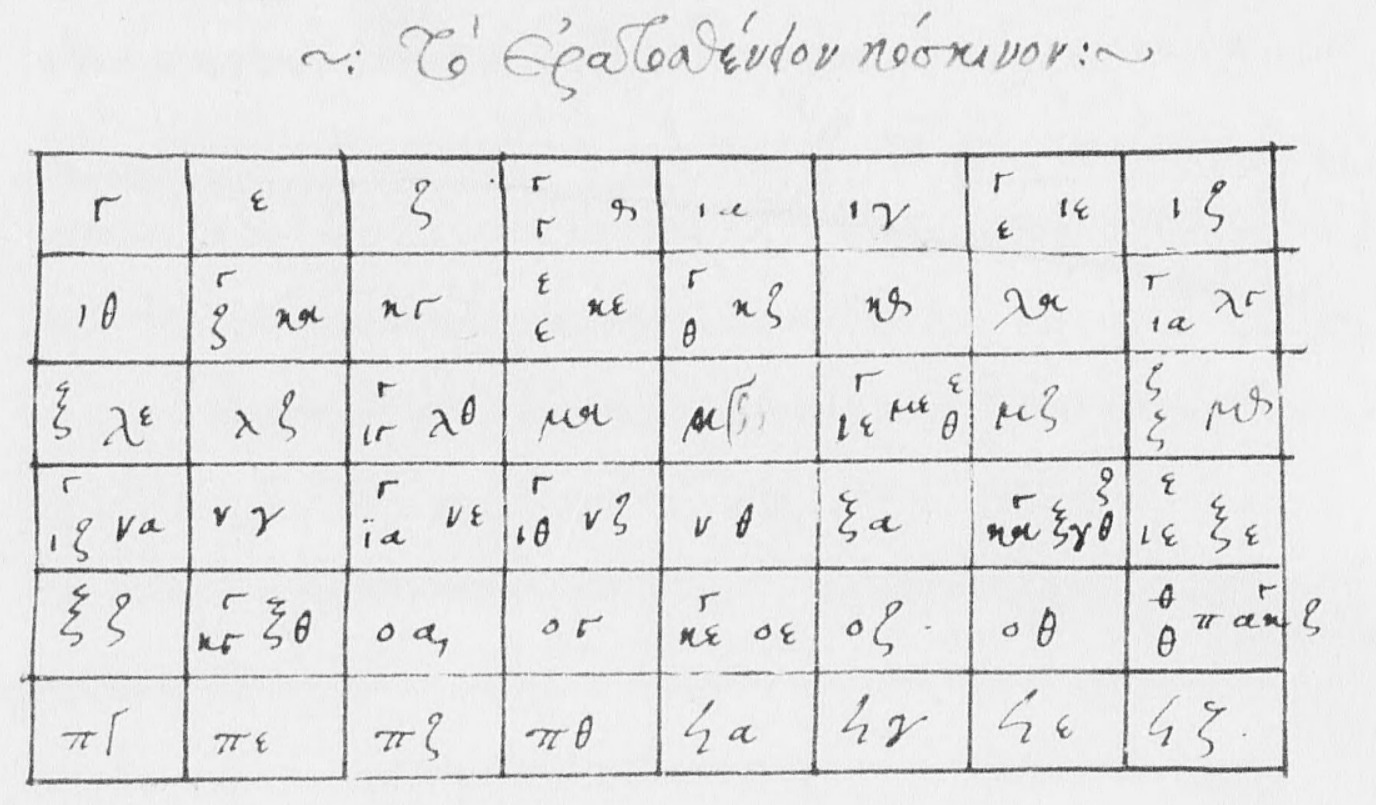
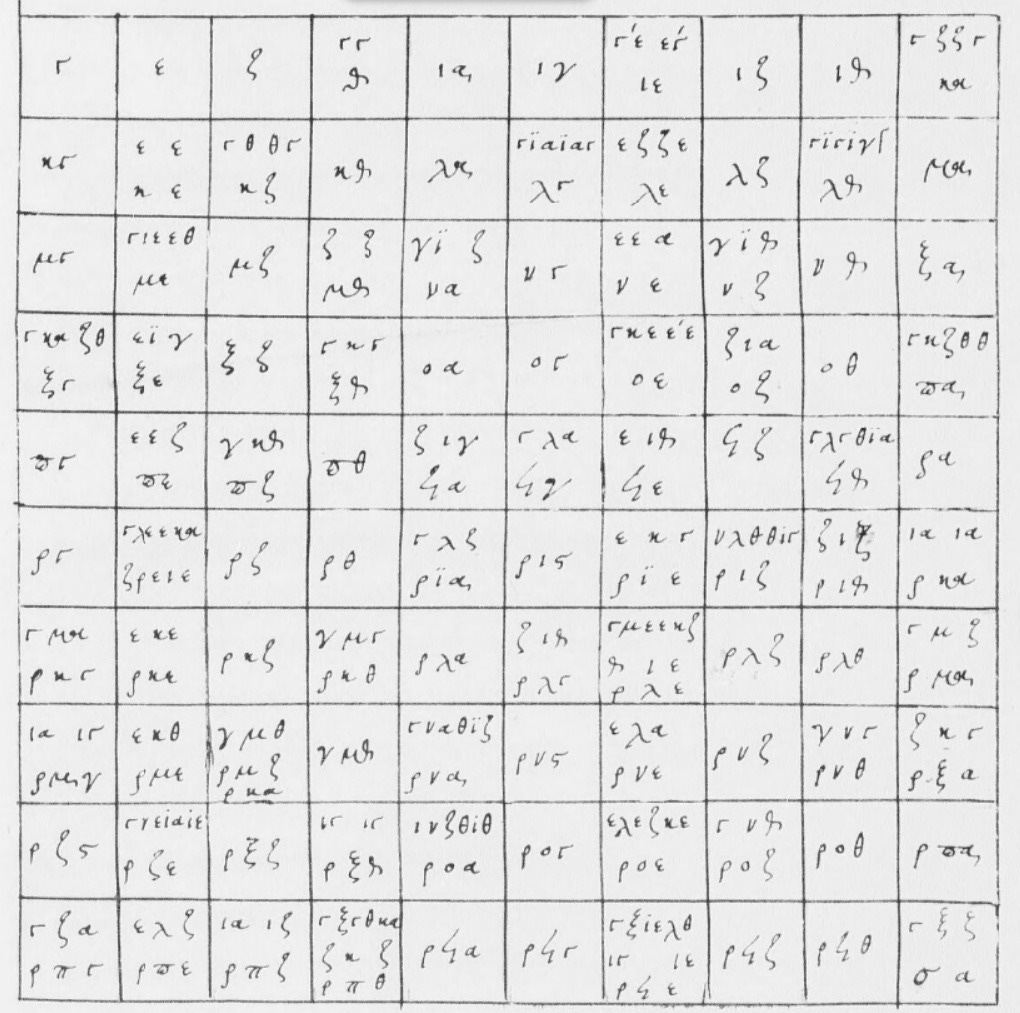
Not such a tidy story! But at least I am able to see evidence of the contamination across manuscripts by studying just the sieves.
The other two 10 × 10 sieves that I found are of higher quality and have no errors in common with those above. Grec 2481, f8v (15th or early 16th century) has a few independent errors: 15 is left unfactorised, there are omissions of 5 × 15 in 75 and 9 × 11 in 99, and 171 has been given a factor of 53 instead of 57. Acerbi’s table says that Grec 2481 is a conformal copy of Vat.gr.1051, f9v (late 13th or early 14th century), a connection which I would not have made. The latter manuscript has been scanned at very low quality; the main grid of odd numbers is almost totally invisible. This is a pity, because the factors are somewhat clear, and I spotted just two scribal errors amongst them, a γ for an α in 33, and a ι for an ε in the factorisation of 165.
In the attached PDF at the end of this post, I collect all the sieves that I found, sorting by grouped family, with generally increasing length. There are 44 sieves, from 35 manuscripts. (I found a further nine manuscripts with at least one unsieved grid of odd numbers, and nineteen manuscripts in which I saw no sieve. Fifty-three manuscripts are either not digitised or not digitised enough to check.)
Scrolling through the PDF, I would describe the collection as mildly interesting – this post is about the journey, not the conclusion. The inline sieves in the commentary are all very similar (I found six of these, and may have missed others), but there are two which are complete in an internally consistent way, two whose multiples of 3 stop at 33, and two which don’t factorise 39.
There are several grids of odd numbers up to 121 – this requires 60 squares, for which there are many possible layouts (ten rows of six, five rows of twelve, etc.). None of these have 121 factorised. Another common size is eight rows of four, showing odd numbers to 65. Again there were some similarities between some pairs of sieves, but overall my impression is that there were a good number of independent recalculations, many abandoned early. In some cases, presumably the original copyist wrote only the starting grid of odd numbers, and someone else did the sieving later.
Were any of the sieves good?
In both the main body of the text and in the image captions, I have been detailing arithmetic errors, lack of completeness, or internal inconsistencies that I’ve found. Some scribes were clearly not paying any attention to the numbers they were copying, some were lazy and abandoned the task early (9, 15, 21, 27, you get the idea). My bar for consistency is fairly high: if in any square, more than one factorisation is shown, then all numbers with more than one distinct factorisation should have all of them shown. A sieve may correctly show the primes while failing this criterion.
The short sieves have an advantage on this latter count, since the only early odd number with two distinct non-trivial factorisations is 45. If the sieve stops before 63 (the next such number), then there will be no internal inconsistency of this type. Two inline sieves to 59 are unobjectional perhaps thanks to this, one of which (Vienna, Cod. Suppl. gr. 169) is clear to read without heavy contrast enhancement.

None of the larger sieves satisfy all my criteria. So:
Supplementary materials
I later found some insurance against this manuscript getting DOGE’d, in the form of a scanned PDF directly from the Karazin eScriptorium.
4o said that Cizensis “does not correspond to any well-known city or monastery traditionally associated with famous codices (like "Codex Vaticanus" or "Codex Sinaiticus".”
It speculated that it might be a fictional place, a rare manuscript in a lesser-known location, or a misspelling or mistranslation.
Except for G2, which most of the time either doesn’t exist or consists of the same atoms as G1.
While my telling of this story is largely chronological, at this point I had only encoded the data and asked o3-mini-high how to make a dendrogram from this kind of data. I left the actual drawing of the plot to be done later.
I am using ‘vibe-code’ in its popular liberal sense – I wrote some of the script myself, reading my encoded data and calculating distances between manuscripts, only copy-pasting from o3-mini-high the dendrogram and associated Matplotlib parts – rather than strictly following Karpathy’s definition.
And in so doing, he avoids a conclusion that only squares of primes would fall into the ‘relatively prime’ category, which he “evidently contemplates”, according to a footnote in D’Ooge. I agree that he contemplates this – his examples are of 9 and 25, and such numbers would stand out on the sieve by virtue of having only one non-trivial factor. A more sophisticated version of what he was tempted by would be a classification into prime, primes raised to a power greater than 1, and composites containing two or more distinct prime factors.